题目内容
6.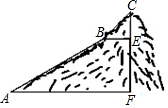 如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)
如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的.其中测得坡长AB=600米,BC=200米,坡角∠BAF=30°,∠CBE=45°.(结果保留根号)
分析 作BG⊥AF于G,在Rt△ABG中根据∠BAF=30°得出BG的长,从而得到EF的长,再在Rt△CBE中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.
解答 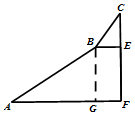 解:如图所示,过B作BG⊥AF于G,
解:如图所示,过B作BG⊥AF于G,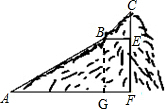
则BG=EF、BE=GF,
∵AB=600,∠BAF=30°,
∴EF=BG=$\frac{1}{2}$AB=300米,
在Rt△BCE中,∵BC=200米,∠CBE=45°,
∴CE=BCsin∠CBE=200×$\frac{\sqrt{2}}{2}$=100$\sqrt{2}$(米),
∴CF=300+100$\sqrt{2}$(米)
∴山峰的高度是(300+100$\sqrt{2}$)米.
点评 本题考查解直角三角形的应用-坡度坡角问题,解题的关键是明确题意,利用锐角三角函数和数形结合的思想解答问题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
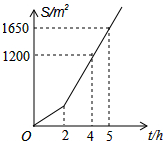 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2.
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是150m2. 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.