题目内容
【题目】如图,已知一次函数![]() 分别交
分别交![]() 、
、![]() 轴于
轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求![]() 、
、![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
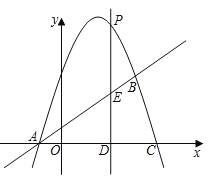
①当![]() 为何值时,线段
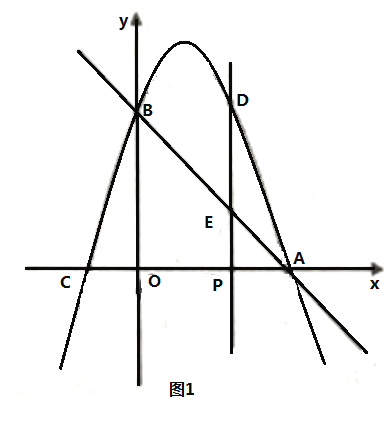
为何值时,线段![]() 长度最大,最大值是多少?(如图1)
长度最大,最大值是多少?(如图1)
②过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,若
,若![]() 与
与![]() 相似,求
相似,求![]() 的值(如图2)
的值(如图2)

【答案】(1)2,3,![]() ;(2)①
;(2)①![]() 时,
时,![]() 长度最大,最大值为
长度最大,最大值为![]() ;②
;②![]() 或
或![]()
【解析】
(1)先求得坐标![]() ,把
,把![]() 代入
代入![]() 中,利用待定系数法求得系数得出解析式,进一步求解
中,利用待定系数法求得系数得出解析式,进一步求解![]() 点坐标即可;
点坐标即可;
(2)①由题知![]() 、
、![]() ;
;![]() 将函数化为顶点式,即可得到最大值.)②将BF、DF用含有t的代数式表示,分类讨论当
将函数化为顶点式,即可得到最大值.)②将BF、DF用含有t的代数式表示,分类讨论当![]() 相似,则
相似,则![]() ,即:
,即: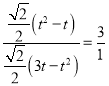 ,求得t,当
,求得t,当![]() 相似,则
相似,则![]() ,即:
,即: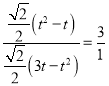 ,求得t即可.
,求得t即可.
解:(1)在![]() 中令
中令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,把
,把![]() 代入
代入![]() 中,得:
中,得:![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() ,
,
∴![]() 点坐标为
点坐标为![]() ;
;
(2)①由题知![]() 、
、![]() ;
;
∴![]()
![]()
![]()
∴当![]() 时,
时,![]() 长度最大,最大值为
长度最大,最大值为![]() .
.
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ;在
;在![]() 中,
中,![]() ,
,![]() ;
;
∴![]()
若![]() 相似,则
相似,则![]() ,即:
,即: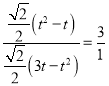 ,
,
解得:![]() (舍去),
(舍去),![]() ;
;
若![]() 相似,则
相似,则![]() ,即:
,即: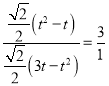 ,解得:
,解得:![]() (舍去),
(舍去),![]() ;综上,
;综上,![]() 或
或![]() 时,
时,![]() 与
与![]() 相似.
相似.

练习册系列答案
相关题目
【题目】在一个不透明的袋子中装有除颜色外其余均相同的m个小球,其中 5 个黑球, 从袋中随机摸出一球,记下其颜色,这称为依次摸球试验,之后把它放回袋 中,搅匀后,再继续摸出一球.以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 | 100 | 1000 | 5000 | 10000 | 50000 | 100000 |
摸出黑球次数 | 46 | 487 | 2506 | 5008 | 24996 | 50007 |
根据列表,可以估计出 m 的值是( )
A. 5 B. 10 C. 15 D. 20