题目内容
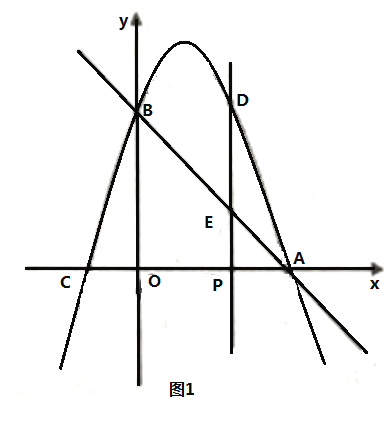
【题目】如图，已知抛物线y＝ax2+bx+c（a≠0）的顶点D坐标为（2，﹣1），且过点B（3，0），与y轴交于点C．
（1）求抛物线的解析式及点C的坐标；
（2）连结OD、CD、CB，CD交x轴于点E，求S△CEB：S△ODE．
【答案】（1）y＝x2﹣4x+3，点C（0，3）；（2）3：1．
【解析】
（1）抛物线的表达式为：y＝a（x﹣2）2﹣1，将点B的坐标代入上式并解得：a＝1，即可求解；
（2）直线CD的表达式为：y＝﹣2x+3，则点E（
，0），S△CEB＝
×EB×OC＝
，S△ODE＝×OE×|yD|＝
，即可求解．
解：（1）抛物线的表达式为：y＝a（x﹣2）2﹣1，
将点B的坐标代入上式并解得：a＝1，
故抛物线的表达式为：y＝x2﹣4x+3，
则点C（0，3）；
（2）将点C、D的坐标代入一次函数表达式：y＝mx+n并解得：
直线CD的表达式为：y＝﹣2x+3，
则点E（，0），
S△CEB＝×EB×OC＝，
S△ODE＝×OE×|yD|＝，
故S△CEB：S△ODE＝3：1．
练习册系列答案
阅读快车系列答案
相关题目
