题目内容
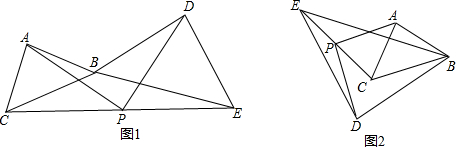
5. 如图,以△ABC的边BC为直径的⊙O分别交AB,AC于D,E,若∠DOE=60°,AD=$\sqrt{2}$,则AC的长为( )
如图,以△ABC的边BC为直径的⊙O分别交AB,AC于D,E,若∠DOE=60°,AD=$\sqrt{2}$,则AC的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 连接CD,根据圆周角定理可得∠ACE=$\frac{1}{2}∠$DOE=30°,∠BDC=90°,再根据直角三角形30°角所对的边等于斜边的一半可得答案.
解答  解:连接CD,如图,
解:连接CD,如图,
∵∠DOE=60°,
∴∠DCE=30°,
∵BC为直径,
∴∠BDC=90°,
∴∠ADC=90°.
∵∠DCE=30°,AD=$\sqrt{2}$,
∴AC=2$\sqrt{2}$,
故选:C.
点评 此题主要考查了圆周角定理,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知a2-5a+1=0,则a+$\frac{1}{a}$-3的值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.
如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.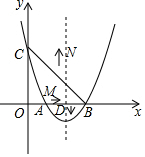 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B(3,0),与y轴交于点C,抛物线的对称轴与x轴交于点D.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B(3,0),与y轴交于点C,抛物线的对称轴与x轴交于点D. 如图,山顶上有高为h的塔BC,从塔顶B测得地面上一点A的俯角是α,从塔底C测得A的俯角为β,求山高H.
如图,山顶上有高为h的塔BC,从塔顶B测得地面上一点A的俯角是α,从塔底C测得A的俯角为β,求山高H.