题目内容
20. 如图,在平面直角坐标系的第一象限中,有一点A(1,2),AB∥x轴且AB=6,点C在线段AB的垂直平分线上,且AC=5,将抛物线y=ax2(a>0)的对称轴右侧的图象记作G.
如图,在平面直角坐标系的第一象限中,有一点A(1,2),AB∥x轴且AB=6,点C在线段AB的垂直平分线上,且AC=5,将抛物线y=ax2(a>0)的对称轴右侧的图象记作G.(1)若G经过C点,求抛物线的解析式;
(2)若G与△ABC有交点.
①求a的取值范围;
②当0<y≤8时,双曲线y=$\frac{k}{x}$经过G上一点,求k的最大值.
分析 (1)如图1中,作CH⊥AB于H.求出点C坐标即可解决问题;
(2)①当抛物线经过点A时,a=2,当抛物线经过点B时,2=49a,可得a=$\frac{2}{49}$,由此即可解决问题;
②由题意当a=$\frac{2}{49}$时,y=$\frac{2}{49}$x2,当y=8时,8=$\frac{2}{49}$x2,因为x>0,推出x=14,由题意当反比例函数y=$\frac{k}{x}$经过点(14,8)时k的值最大;
解答 解:(1)如图1中,作CH⊥AB于H.
∵CA=CB=5,CH⊥AB,
∴AH=HB=3,
在Rt△ACH中,CH=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴C(4,6),
∵抛物线y=ax2(a>0)经过C点,
∴6=16a,
∴a=$\frac{3}{8}$,
∴抛物线的解析式为y=$\frac{3}{8}$x2.
(2)①∵A(1,2),B(7,2),
当抛物线经过点A时,a=2,
当抛物线经过点B时,2=49a,
∴a=$\frac{2}{49}$,
∵若G与△ABC有交点,
∴$\frac{2}{49}$≤a≤2.
②由题意当a=$\frac{2}{49}$时,y=$\frac{2}{49}$x2,
当y=8时,8=$\frac{2}{49}$x2,
∴x>0,
∴x=14,
∴当反比例函数y=$\frac{k}{x}$经过点(14,8)时k的值最大,此时k=112,
∴k的最大值为112.
点评 本题考查二次函数综合题、待定系数法、勾股定理等知识,解题的关键是理解题意,学会利用特殊点解决问题,属于中考压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
 在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.| A. | 100 | B. | 110 | C. | 120 | D. | 130 |
12.国务院总理李克强在《2017年国务院政府工作报告》中提到,2016年新增第四代移动通信用户3.4亿,数据“3.4亿”用科学记数法表示为( )
| A. | 3.4×106 | B. | 3.4×108 | C. | 34×107 | D. | 3.4×109 |
 在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC.
在平面直角坐标系中,抛物线y=ax2+bx-3经过点A(-1,0)和点B(2,-1),交y轴于点C,BD⊥x轴于点D,连接AB、AC.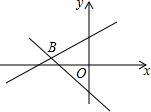 一次函数y=ax+3与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax-bx+3>-1的解集表示在数轴上正确的是( )
一次函数y=ax+3与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax-bx+3>-1的解集表示在数轴上正确的是( )



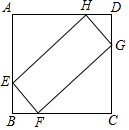 如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,
如图,正方形ABCD,AB=8,点E,F,G,H分别在正方形ABCD的边上(不与正方形的顶点重合),设BF=m,EF:FG=1:k,其中k≥1,若四边形EFGH是矩形,



 如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )
如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( )