题目内容
20. 如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )| A. | $\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{4π}{3}$-2$\sqrt{3}$ | C. | π-$\sqrt{3}$ | D. | $\frac{2π}{3}$-$\sqrt{3}$ |
分析 过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解.
解答 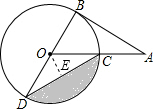 解:过O点作OE⊥CD于E,
解:过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∵⊙O的半径为2,
∴OE=1,CE=DE=$\sqrt{3}$,
∴CD=2$\sqrt{3}$,
∴图中阴影部分的面积为:$\frac{120×π×{2}^{2}}{360}$-$\frac{1}{2}$×2$\sqrt{3}$×1=$\frac{4}{3}$π-$\sqrt{3}$.
故选:A.
点评 考查了扇形面积的计算,切线的性质,本题关键是理解阴影部分的面积=扇形OCD的面积-三角形OCD的面积.

练习册系列答案
相关题目
15.月球的半径约为1738000m,1738000这个数用科学记数法可表示为( )
| A. | 1.738×106 | B. | 1.738×107 | C. | 0.1738×107 | D. | 17.38×105 |
9.在0,-2,5,$\frac{1}{4}$,-0.3中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.顺次连接矩形ABCD各边中点,所得四边形必定是( )
| A. | 邻边不等的平行四边形 | B. | 矩形 | ||
| C. | 正方形 | D. | 菱形 |
 如图,∠1=∠2,∠A=60°,则∠ADC=120度.
如图,∠1=∠2,∠A=60°,则∠ADC=120度.