题目内容
5.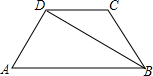 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=3cm,∠A=60°,BD平分∠ABC,则梯形的周长( )cm.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=3cm,∠A=60°,BD平分∠ABC,则梯形的周长( )cm.| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
分析 根据等腰梯形的性质求出∠ABC=∠A=60°,求出∠CDB=∠CBD=∠ABD=30°,根据等腰三角形的判定得出DC=BC,求出AB=2AD,即可求出答案.
解答 解:∵四边形ABCD是等腰梯形,DC∥AB,∠A=60°,
∴∠CBA=∠A=60°,
∵BD平分∠CBA,
∴∠CBD=∠ABD=30°
∵AB∥CD,
∴∠CDB=∠ABD=30°,
∴∠CDB=∠CBD=30°,
∴DC=BC=3cm,
∵∠A=60°,∠ABD=30°,
∴∠ADB=90°,
∴AB=2AD=6cm,
∴梯形ABCD的周长为AD+DC+BC+AB=3cm+3cm+3cm+6cm=15cm.
故选B.
点评 本题考查了等腰梯形的性质,等腰三角形的判定,含30°角的直角三角形的性质,三角形内角和定理的应用,能求出AB=2AD和DC=BC是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下列各式正确的是( )
| A. | $\frac{6}{7}$<$\frac{5}{6}$ | B. | -|-5|>-4 | C. | -$\frac{5}{6}$<-$\frac{4}{5}$ | D. | -$\frac{5}{4}$>-1.25 |
17.下列各组中,两个单项式是同类项的是( )
| A. | 3mn与-4nm | B. | -mn2与m2n | C. | 2x3与-3y3 | D. | 3ab与-abc |

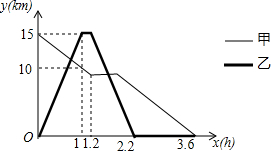 某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.


