Question

【题目】阅读理解

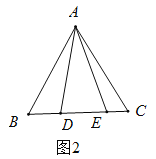
（1）如图1，在中，，，，为边上的点，且，若，，求的长．

思考如下：注意到条件中有，，不妨把绕点顺时针旋转，得到，连接，易证，从而将线段，，集中在了中，因为的度数是________；，所以的长为 ；

类比探究

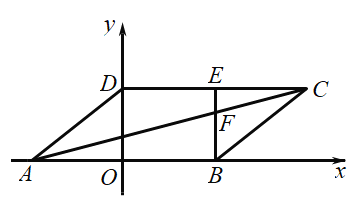
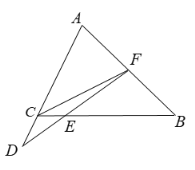
（2）如图2，在中，，，，为边上的点，且，，，求的长；

拓展应用

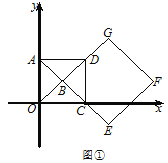
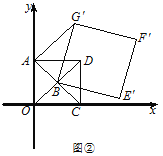
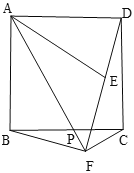
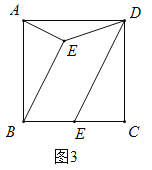
（3）如图3，是正方形内一点，，是边上一点，且，若，请直接写出当取最小值时的长．

Answer 1

【答案】（1）；；（2）；（3）

【解析】

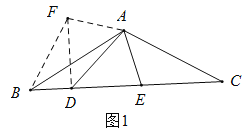
（1）根据旋转的性质可得△ACE≌△ABF，△ADE≌△ADF，得∠ABF=∠ACE=30°, DE=DF，再证明△BDF是直角三角形，运用勾股定理求出DF的长即可得到结论；

（2）将绕点逆时针旋转，得到，连接，CF, 过点作交的延长线于点，方法同（1）证明得，求出FG和CG的长，再运用勾股定理即可EF的长，从而得到结论；

（3）将绕点顺时针旋转，得到取的中点连接，取最小值时，点在上，方法同（2）可证明得OF=OG，在真的三角形BOF中运用勾股定理可求出结论.

（1）∵AB=AC，∠BAC=120°

∴∠ABC=∠ACB=30°

把绕点顺时针旋转，得到，

∴△ABF≌△ACE

∴∠ABF=∠ACE=30°

∴∠FBD=60°；

连接，

∵∠BAC=120°，∠DAE=60°，

∴∠BAD+∠CAE=60°

∵∠BAF=∠CAE，

∴∠BAF+∠BAD=60°，即∠DAF=60°

∴∠DAF=∠DAE，

又AF=AE，AD=AD，

∴△DAF≌△DAE，

∴DF=DE

∵BD=1，BF=CE=2，且∠FBD=60°

∴∠BFD=30°，

∴∠BDF=90°，

∴

∴DE=

故答案为：60；；

（2）∵，，

∴是等边三角形，

∴，

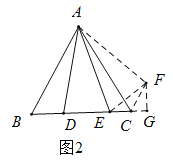
如图2 ，将绕点逆时针旋转，得到连接

则.

又

.

如图2，过点作交的延长线于点.

在中，

在中，

.

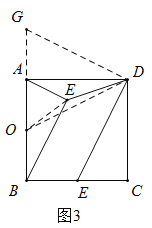
（3）如图3，将绕点顺时针旋转，得到

取的中点连接.

因为，

所以取最小值时，点在上

由类比，得.

设的长为

则.

所以，

解得

∴.