题目内容
15.有一块直角三角形绿地,量得两直角边长为6m,8m,现在要将绿地扩充成等腰三角形,且扩充时只能延长6m的直角边,则扩充后等腰三角形绿地的面积为32或40m2.分析 由于扩充所得的等腰三角形腰和底不确定,若设扩充所得的三角形是△ABD,则应分为①AC=CD,②AD=AB,2种情况进行讨论.
解答 解:∵两直角边长为6m,8m,
∴由勾股定理得到:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10m.
①如图1: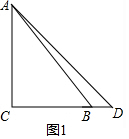
当AC=CD=8m时;
∵AC⊥CB,
此时等腰三角形绿地的面积:$\frac{1}{2}$×8×8=32(m2);
②如图2,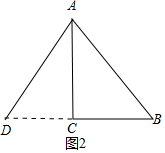
延长BC到D使BC=CD=6m,
此时AB=AD=10m,
此时等腰三角形绿地的面积:$\frac{1}{2}$×12×8=48(m2);
③延长BC到D使BD=AB=10m,
此时等腰三角形绿地的面积:$\frac{1}{2}$×10×8=40(m2);
综上所述,扩充后等腰三角形绿地的面积为32m2或48m2或40m2.
故答案是:32或40.
点评 此题主要考查了等腰三角形的性质以及勾股定理的应用,解决问题的关键是根据题意正确画出图形.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
10.抛物线y=x2-2x+1的对称轴是( )
| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=2 | D. | 直线x=-2 |
20.数a四舍五入后的近似值为3.1,则a的取值范围是( )
| A. | 3.0≤a≤3.2 | B. | 3.14≤a<3.15 | C. | 3.144≤a<3.149 | D. | 3.05≤a<3.15 |