题目内容
如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.
(1)使∠APB=30°的点P有 个;
(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标;
(3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,也请说明理由.
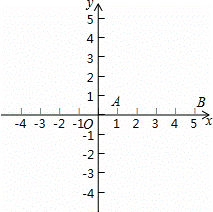
解:(1)以AB为边,在第一象限内作等边三角形ABC,
以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.
在优弧AP1B上任取一点P,如图1,
则∠APB= ∠ACB=
∠ACB= ×60°=30°.
×60°=30°.
∴使∠APB=30°的点P有无数个.
故答案为:无数.
(2)①当点P在y轴的正半轴上时,
过点C作CG⊥AB,垂足为G,如图1.
∵点A(1,0),点B(5,0),
∴OA=1,OB=5.
∴AB=4.
∵点C为圆心,CG⊥AB,
∴AG=BG= AB=2.
AB=2.
∴OG=OA+AG=3.
∵△ABC是等边三角形,
∴AC=BC=AB=4.
∴CG=
=
=2 .
.
∴点C的坐标为(3,2 ).
).
过点C作CD⊥y轴,垂足为D,连接CP2,如图1,
∵点C的坐标为(3,2 ),
),
∴CD=3,OD=2 .
.
∵P1、P2是⊙C与y轴的交点,
∴∠AP1B=∠AP2B=30°.
∵CP2=CA=4,CD=3,
∴DP2= =
= .
.
∵点C为圆心,CD⊥P1P2,
∴P1D=P2D= .
.
∴P2(0,2 ﹣
﹣ ).P1(0,2
).P1(0,2 +
+ ).
).
②当点P在y轴的负半轴上时,
同理可得:P3(0,﹣2 ﹣
﹣ ).P4(0,﹣2
).P4(0,﹣2 +
+ ).
).
综上所述:满足条件的点P的坐标有:
(0,2 ﹣
﹣ )、(0,2
)、(0,2 +
+ )、(0,﹣2
)、(0,﹣2 ﹣
﹣ )、(0,﹣2
)、(0,﹣2 +
+ ).
).
(3)当过点A、B的⊙E与y轴相切于点P时,∠APB最大.
①当点P在y轴的正半轴上时,
连接EA,作EH⊥x轴,垂足为H,如图2.
∵⊙E与y轴相切于点P,
∴PE⊥OP.
∵EH⊥AB,OP⊥OH,
∴∠EPO=∠POH=∠EHO=90°.
∴四边形OPEH是矩形.
∴OP=EH,PE=OH=3.
∴EA=3.
∵∠EHA=90°,AH=2,EA=3,
∴EH=
=
=
∴OP=
∴P(0, ).
).
②当点P在y轴的负半轴上时,
同理可得:P(0,﹣ ).
).
理由:
①若点P在y轴的正半轴上,
在y轴的正半轴上任取一点M(不与点P重合),
连接MA,MB,交⊙E于点N,连接NA,如图2所示.
∵∠ANB是△AMN的外角,
∴∠ANB>∠AMB.
∵∠APB=∠ANB,
∴∠APB>∠AMB.
②若点P在y轴的负半轴上,
同理可证得:∠APB>∠AMB.
综上所述:当点P在y轴上移动时,∠APB有最大值,
此时点P的坐标为(0, )和(0,﹣
)和(0,﹣ ).
).



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案某销售公司有营销人员15人,销售部为了制定某种商品的月销售量定额,统计了这15人某月的销售量,如下表所示:
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
那么这15位销售人员该月销售量的平均数、众数、中位数分别是( )
|
| A. | 320,210,230 | B. | 320,210,210 | C. | 206,210,210 | D. | 206,210,230 |
在函数y= 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
|
| A. | x≥﹣2且x≠1 | B. | x≤2且x≠1 | C. | x≠1 | D. | x≤﹣2 |






 mm2 C.7×10-7 mm2
mm2 C.7×10-7 mm2  D.70×10-8 mm2
D.70×10-8 mm2