题目内容
如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这 两个直角三角形能够拼成一个等腰三角形.
两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)求出4种不同拼法的图形的等腰三角形的周长.
解:(1)4种不同拼法(周长不等)的等腰三角形如图所示:

(2)图1:拼成的等腰三角形的周长为10+6+4+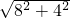 =20+4
=20+4 ;
;
图2:拼成的等腰三角形的周长为10+10+12=32;
图3:根据图示知,
64+x2=(x+6)2,
解得,x= ,
,
∴拼成的等腰三角形的周长为2×( +6)+10=
+6)+10= ;
;
图4:拼成的等腰三角形的周长为10+10+8+8=36.
分析:(1)根据三角形的三边关系、勾股定理的逆定理和等腰三角形的判定来作图;
(2)利用(1)的图形,分别求得每一个等腰三角形的周长.
点评:本题考查了勾股定理的逆定理、等腰三角形的判定.解题时,采用了“分类讨论”的数学思想.

(2)图1:拼成的等腰三角形的周长为10+6+4+
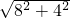 =20+4
=20+4 ;
;图2:拼成的等腰三角形的周长为10+10+12=32;
图3:根据图示知,
64+x2=(x+6)2,
解得,x=
 ,
,∴拼成的等腰三角形的周长为2×(
 +6)+10=
+6)+10= ;
;图4:拼成的等腰三角形的周长为10+10+8+8=36.
分析:(1)根据三角形的三边关系、勾股定理的逆定理和等腰三角形的判定来作图;
(2)利用(1)的图形,分别求得每一个等腰三角形的周长.
点评:本题考查了勾股定理的逆定理、等腰三角形的判定.解题时,采用了“分类讨论”的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
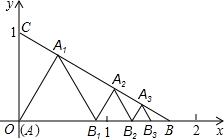 如图,已知点A(0,0),
如图,已知点A(0,0),


 如图,已知△ABC是一个等边三角形,它的边AB长为3,D、E、F分别是AB、BC、CA的三等分点,则△DEF的边长为
如图,已知△ABC是一个等边三角形,它的边AB长为3,D、E、F分别是AB、BC、CA的三等分点,则△DEF的边长为 ,
, ,
, ,在
,在 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在 轴上,另一个顶点在
轴上,另一个顶点在 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个 ,第2个
,第2个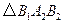 ,第3个
,第3个 ,…,则第1个等边三角形的边长等于 , 第
,…,则第1个等边三角形的边长等于 , 第 (
( ,且
,且