题目内容
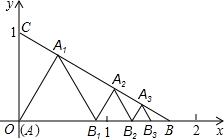 如图,已知点A(0,0),B(
如图,已知点A(0,0),B(| 3 |
分析:根据题目已知条件可推出,AA1=
OC=
,B1A2=
A1B1=
×
=
,依此类推,第n个等边三角形的边长等于
.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 22 |
| ||
| 2n |
解答:解:∵OB=
,OC=1,
∴BC=2,
所以第1个等边三角形的边长等于AA1=
OC=
,
∴∠OBC=30°,∠OCB=60°.
而△AA1B1为等边三角形,∠A1AB1=60°,
∴∠COA1=30°,则∠CA1O=90°.
在Rt△CAA1中,AA1=
OC=
,
同理得:B1A2=
A1B1=
,
依此类推,第n个等边三角形的边长等于
.
故答案为:
,
.
| 3 |
∴BC=2,
所以第1个等边三角形的边长等于AA1=
| ||
| 2 |
| ||
| 2 |
∴∠OBC=30°,∠OCB=60°.
而△AA1B1为等边三角形,∠A1AB1=60°,
∴∠COA1=30°,则∠CA1O=90°.
在Rt△CAA1中,AA1=
| ||
| 2 |
| ||
| 2 |
同理得:B1A2=
| ||
| 2 |
| ||
| 22 |
依此类推,第n个等边三角形的边长等于
| ||
| 2n |
故答案为:
| ||
| 2 |
| ||
| 2n |
点评:本题主要考查等边三角形的性质及解直角三角形,从而归纳出边长的规律.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )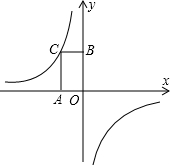 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=