题目内容
如图，AB与⊙O相切于点B，AO=6cm，AB=4cm，则⊙O的半径为
分析：连接OB，则OB⊥AB；在Rt△AOB中，利用勾股定理可得到OB的值．
解答：
解：连接OB，
∵AB与⊙O相切于点B，∴OB⊥AB，
在Rt△AOB中，AO=6，AB=4，
∴OB=
=
=2
（cm）．
故答案是：2
cm．
解：连接OB，∵AB与⊙O相切于点B，∴OB⊥AB，
在Rt△AOB中，AO=6，AB=4，
∴OB=
| AO2-AB2 |
| 62-42 |
| 5 |
故答案是：2
| 5 |
点评：此题主要考查圆的切线的性质及勾股定理的应用．通过切线的性质定理得到△AOB是直角三角形，是解决本题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
9、如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C=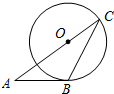
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC．若∠A=48°，则∠C=
已知：如图，AB与⊙O相切于点C，OA=OB，⊙O的直径为4，AB=8．则sinA的值是
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=36°，则∠C=