题目内容
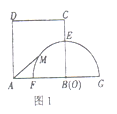
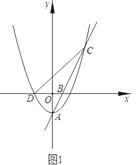
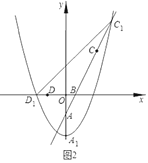
【题目】已知函数y= 的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.
的图象如图所示,若直线y=x+m与该图象恰有三个不同的交点,则m的取值范围为_____.

【答案】0<m<![]()
【解析】
由直线y=x+m与该图象恰有三个不同的交点可知直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x有两个交点,分别联立两个解析式求出m的取值范围即可得答案.
∵直线y=x+m与该图象恰有三个不同的交点,
∴直线y=x+m与y=-x(x≤0)有一个交点,与y=-x2+2x(x>0)有两个交点,
x+m=-x
x=![]() ,
,
∵x≤0,
∴m≥0,
-x2+2x=x+m,
x2-x+m=0,
∵y=x+m与y=-x2+2x(x>0)有两个交点,
∴△=(-1)2-4m>0,
解得:m<![]() ,
,
∵当m=0时,直线y=x+m过(0,0)点,
∴与y= 图象只有两个交点,
图象只有两个交点,
∴m≠0,
∴m的取值范围为:0<m<![]() .
.
故答案为:0<m<![]()

练习册系列答案
相关题目
【题目】为了解全区3000名九年级学生英语听力口语自动化考试成绩的情况,随机抽取了部分学生的成绩(满分30分且得分均为整数),制成下表:
分数段(x分分) | 0≤x≤18 | 19≤x≤21 | 22≤x≤24 | 25≤x≤27 | 28≤x≤30 |
人数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数所在的分数段是 ;
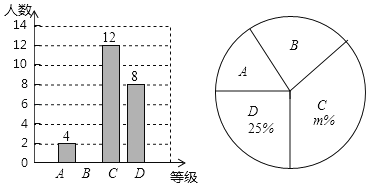
③若用扇形统计图表示统计结果,则分数段为0≤x≤18的人数所对应扇形的圆心角为 °;
(2)如果将25分以上(含25分)定为优秀,请估计全区九年级考生成绩为优秀的人数.