题目内容
19.阅读下面材料:在小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为5,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,
①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为15;
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长不变(填“改变”或“不变”).
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为5,改变∠ABC的大小,折痕EF的长为m.
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为10+5$\sqrt{3}$;
(2)如图4,若∠ABC的大小为β,则六边形AEFCHG的周长可表示为10+10sin$\frac{β}{2}$.

分析 ①根据题意可知△BEF和△DGH是等边三角形,再根据菱形的性质即可求解;
②根据题意可知△BEF和△DGH是等边三角形,再根据菱形的性质即可求解;
(1)根据题意可知EF+GH=AC,再根据三角函数和菱的性质即可求解;
(2)根据题意可知EF+GH=AC,再根据三角函数和菱形的性质即可求解.
解答 解:①当重合点在菱形的对称中心O处时,
由题意可知:△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=5+5+5=15.
∴六边形AEFCHG的周长为15;
故答案为:15;
②不变;理由如下:
当重合点在对角线BD上移动时,
由题意可知△BEF和△DGH是等边三角形,
∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=5+5+5=15.
∴六边形AEFCHG的周长为15.
故六边形AEFCHG的周长不变.
(1)若∠ABC=120°,
由题意可知:EF+GH=AC,
则六边形AEFCHG的周长为2×5+2×sin60°×5=10+5$\sqrt{3}$;
故答案为:10+5$\sqrt{3}$;
(2)若∠ABC的大小为β,
由题意可知:EF+GH=AC,
则六边形AEFCHG的周长可表示为2×5+2×sin$\frac{β}{2}$×5=10+10sin$\frac{β}{2}$.
故答案为:10+10sin$\frac{β}{2}$.
点评 本题是四边形综合题目,考查了翻折变换(折叠问题),等边三角形的判定与性质,六边形的性质,菱形的性质以及三角函数等知识;本题关键是得到EF+GH=AC,综合性较强,有一定的难度.

练习册系列答案
相关题目
9. 如图是某个几何体的三视图,该几何体为( )
如图是某个几何体的三视图,该几何体为( )
 如图是某个几何体的三视图,该几何体为( )
如图是某个几何体的三视图,该几何体为( )| A. | 长方体 | B. | 四面体 | C. | 圆柱体 | D. | 四棱锥 |
10.下列四个几何体中,主视图为圆的是( )
| A. | 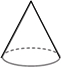 | B. |  | C. | 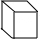 | D. | 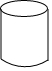 |
14.下列多项式乘法能用平方差公式进行计算的是( )
| A. | (a+b)(b+a) | B. | (a+b)(-a-b) | C. | (a-b)(b-a) | D. | (a-b)(b+a) |
4.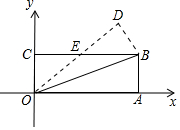 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
 如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )| A. | $y=\frac{4}{5}x$ | B. | $y=\frac{5}{4}x$ | C. | $y=\frac{3}{4}x$ | D. | $y=\frac{4}{3}x$ |
9.中国人最早使用负数,可追溯到两千多年前的秦汉时期,-0.5的相反数是( )
| A. | 0.5 | B. | ±0.5 | C. | -0.5 | D. | 5 |
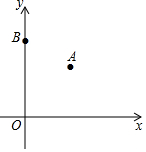 如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )
如图,在平面直角坐标系中,已知点A(3,3),B(0,5),若在坐标轴上找一点C,使得△ABC是等腰三角形,则这样的点C有( )