题目内容
当x取任意实数时,y=-(x-3)2+1,
当x= 时,有最 值 ;
当-2≤x≤5时,当x= 时,有最大值为 ,最小值为 ;
当-2≤x≤2时,当x= 时,有最大值为 ;最小值为 .
当x=
当-2≤x≤5时,当x=
当-2≤x≤2时,当x=
考点:二次函数的最值
专题:
分析:根据抛物线的开口方向判定抛物线y=-(x-3)2+1有最大值;根据抛物线的解析式求得抛物线与y轴的交点坐标,作出草图,根据抛物线的增碱性回答问题.
解答: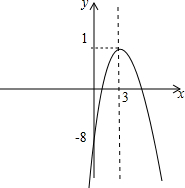 解:∵y=-(x-3)2+1,
解:∵y=-(x-3)2+1,
∴该抛物线的顶点坐标是(3,1),且开口方向向下.
又∵当x=0时,y=-(0-3)2+1=-8,
∴该抛物线与y轴的交点坐标是(0,-8).
∴其大致图象如图所示:
在x=3时,y有最大值为1;
在-2≤x≤5上,当x=3时,y有最大值为1,x=-2时,y最小值=-(-2-3)2+1=-24
在-2≤x≤2上,y随x的增大而增大,则当x=2时,y最大=-(2-3)2+1=0.x=-2时,y最小值=-(-2-3)2+1=-24
故答案是:3;大;1;3;1;-24;2;0;-24.
 解:∵y=-(x-3)2+1,
解:∵y=-(x-3)2+1,∴该抛物线的顶点坐标是(3,1),且开口方向向下.
又∵当x=0时,y=-(0-3)2+1=-8,
∴该抛物线与y轴的交点坐标是(0,-8).
∴其大致图象如图所示:
在x=3时,y有最大值为1;
在-2≤x≤5上,当x=3时,y有最大值为1,x=-2时,y最小值=-(-2-3)2+1=-24
在-2≤x≤2上,y随x的增大而增大,则当x=2时,y最大=-(2-3)2+1=0.x=-2时,y最小值=-(-2-3)2+1=-24
故答案是:3;大;1;3;1;-24;2;0;-24.
点评:本题考查了二次函数的最值.确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标;当自变量取某个范围时,要分别求出顶点和函数端点处的函数值,比较这些函数值,从而获得最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果存入500元记为+500元,那么支出300元记为( )
| A、+300元 |
| B、-300元 |
| C、+200元 |
| D、-200元 |
 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC,垂足为E,若∠B=40°,∠C=70°.求∠ADE的度数.
如图,在△ABC中,AD是∠BAC的平分线,DE⊥AC,垂足为E,若∠B=40°,∠C=70°.求∠ADE的度数.