题目内容
7. 如图,在△ABC中,E,D,F分别是AB,BC,CA的中点,AC=4,BC=5,AB=6,则四边形AEDF的周长是10.
如图,在△ABC中,E,D,F分别是AB,BC,CA的中点,AC=4,BC=5,AB=6,则四边形AEDF的周长是10.
分析 先根据中点的性质得出AE与AF的长,再由三角形中位线定理求出DE及DF的长,进而可得出结论.
解答 解:∵E,F分别是AB,CA的中点,AC=4,AB=6,
∴AE=$\frac{1}{2}$AB=3,AF=$\frac{1}{2}$AC=2.
∵D是BC的中点,
∴DE=$\frac{1}{2}$AC=2,DF=$\frac{1}{2}$AB=3,
∴四边形AEDF的周长=AE+DE+DF+AF=3+2+3+2=10.
故答案为:10.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )
如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°,则∠3=( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
15.分别写有数0,2-1,-2,cos30°,3的五张卡片,除数字不同外其他均相同,从中任意抽取一张,那么抽到非负数的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
2. 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )
 如图,直线b、c被直线a所截,则∠1与∠2是( )
如图,直线b、c被直线a所截,则∠1与∠2是( )| A. | 同位角 | B. | 同旁内角 | C. | 内错角 | D. | 对顶角 |
16.下列计算中,正确的是( )
| A. | $\root{3}{8}$=±2 | B. | $\root{6}{(-2)^{6}}$=$\root{3}{(-2)^{3}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | ($\frac{1}{64}$)${\;}^{\frac{1}{6}}$=$\frac{1}{2}$ |
17.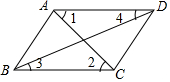 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )
 如图,下列条件中不能判定AD∥BC的是( )
如图,下列条件中不能判定AD∥BC的是( )| A. | ∠BAD+∠ABC=180° | B. | ∠1=∠2 | C. | ∠3=∠4 | D. | ∠BAD=∠BCD |