题目内容
 如图,在梯形ABCD中,AD∥BC,AC=BD,梯形ABCD是等腰梯形吗?为什么?
如图,在梯形ABCD中,AD∥BC,AC=BD,梯形ABCD是等腰梯形吗?为什么?考点:等腰梯形的判定
专题:
分析:过A作AE∥BD交CB的延长线与E,推出∠E=∠DBC,四边形AEBD是平行四边形,求出∠E=∠ACB=∠DBC,根据SAS推出△ABC≌△DCB,推出AB=DC,根据等腰梯形的判定得出即可.
解答:解:四边形ABCD是等腰梯形,
理由是:过A作AE∥BD交CB的延长线与E,
则∠E=∠DBC,
∵AD∥BC,
∴四边形AEBD是平行四边形,
∴AE=BD,
∵AC=BD,
∴AE=AC,
∴∠E=∠ACB=∠DBC,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS),
∴AB=DC,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.

理由是:过A作AE∥BD交CB的延长线与E,
则∠E=∠DBC,
∵AD∥BC,
∴四边形AEBD是平行四边形,
∴AE=BD,
∵AC=BD,
∴AE=AC,
∴∠E=∠ACB=∠DBC,
在△ABC和△DCB中,
|
∴△ABC≌△DCB(SAS),
∴AB=DC,
∵四边形ABCD是梯形,
∴四边形ABCD是等腰梯形.
点评:本题考查了平行四边形的性质和判定,等腰梯形的判定,全等三角形的性质和判定的应用,解此题的关键是能正确作出辅助线,并进一步推出AB=CD,注意:两腰相等的梯形是等腰梯形.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 将一副三角板按如图方式摆放在一起,且∠1比∠2大30°,则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,且∠1比∠2大30°,则∠1的度数等于( )| A、30° | B、60° |
| C、70° | D、80° |
 图中共有线段( )
图中共有线段( )| A、8条 | B、9条 |
| C、10条 | D、11条 |
下列说法:①若-1<b<0,则b>
;②若∠AOP=∠BOP,则OP平分∠AOB;③同旁内角互补,那么它们的两条角平分线互相垂直;④两条直线相交有且只有一个交点,其中正确的个数是( )
| 1 |
| b |
| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,把各边都缩小到
,那么sinA的值( )
| 1 |
| 5 |
A、都缩小
| ||
| B、都不变 | ||
| C、都扩大5倍 | ||
| D、无法确定 |
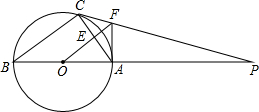 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF. 如图,已知∠AOB=50°,OC平分∠AOB
如图,已知∠AOB=50°,OC平分∠AOB 如图,△AOB中,A、B两点的坐标分别为(3,4),(6,2).
如图,△AOB中,A、B两点的坐标分别为(3,4),(6,2). 如图,在△ABC中,直线l、m、n分别是三边的垂直平分线,其中l、m交于点O.求证:直线n经过点O.
如图,在△ABC中,直线l、m、n分别是三边的垂直平分线,其中l、m交于点O.求证:直线n经过点O.