题目内容
点D,E分别是△ABC的边AB,AC的中点,则S△ADE:S△ABC
- A.

- B.

- C.

- D.

C
分析:利用三角形中位线定理,可知DE∥BC,那么△ADE∽△ABC,再利用相似三角形的面积比等于相似比的平方可求.
解答: 解:∵点D,E分别是△ABC的边AB,AC的中点,
解:∵点D,E分别是△ABC的边AB,AC的中点,
∴DE∥BC,DE= BC,AD=
BC,AD= AB,AE=
AB,AE= AC
AC
即 =
= =
= =
= ,
,
∴△ADE∽△ABC,相似比为 ,
,
故S△ADE:S△ABC=1:4.
故选C.
点评:本题考查对相似三角形性质及三角形的中位线定理的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
三角形的中位线定理:三角形的中位线平行于底边且等于底边的一半.
分析:利用三角形中位线定理,可知DE∥BC,那么△ADE∽△ABC,再利用相似三角形的面积比等于相似比的平方可求.
解答:
 解:∵点D,E分别是△ABC的边AB,AC的中点,
解:∵点D,E分别是△ABC的边AB,AC的中点,∴DE∥BC,DE=
 BC,AD=
BC,AD= AB,AE=
AB,AE= AC
AC即
 =
= =
= =
= ,
,∴△ADE∽△ABC,相似比为
 ,
,故S△ADE:S△ABC=1:4.
故选C.
点评:本题考查对相似三角形性质及三角形的中位线定理的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.
三角形的中位线定理:三角形的中位线平行于底边且等于底边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,已知BC=
如图所示,已知BC=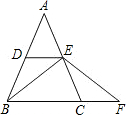 如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF=
如图,在△ABC中,AB=AC,点D,E分别是AB,AC的中点,F是BC延长线上的一点,且CF= 7、如图,AB=AC,点D、E分别是AB、AC上的点.若再添加一个条件使得△ABE≌△ACD,则以下四个选项不能作为添加的条件的是( )
7、如图,AB=AC,点D、E分别是AB、AC上的点.若再添加一个条件使得△ABE≌△ACD,则以下四个选项不能作为添加的条件的是( ) 18、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.求证:四边形DBCF是平行四边形.
18、如图,在△ABC中,点D,E分别是AB,AC边的中点,若把△ADE绕着点E顺时针旋转180°得到△CFE.求证:四边形DBCF是平行四边形.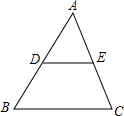 (2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=
(2013•邵阳)如图所示,在△ABC中,点D、E分别是AB、AC的中点,连结DE,若DE=5,则BC=