题目内容
已知一元二次方程x2-3x+m-1=0.若方程有两个相等的实数根,求此方程的解.
考点:根的判别式
专题:
分析:根据一元二次方程x2-3x+m-1=0有两个相等的实数根,得出△=b2-4ac=0,再代入求解即可.
解答:解:∵一元二次方程x2-3x+m-1=0有两个相等的实数根,
∴△=b2-4ac=0,
即:(-3)2-4(m-1)=0,
解得:m=
.
∴△=b2-4ac=0,
即:(-3)2-4(m-1)=0,
解得:m=
| 13 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
下列方程是一元二次方程的是( )
A、3x+
| ||
| B、x2+y2=5 | ||
| C、3x-5=4 | ||
| D、3x2-x=0 |
下列各组数中,互为相反数的是( )
A、-2与-
| ||||
| B、|-2|与2 | ||||
C、-
| ||||
D、-
|
抛物线y=2x2,y=-2x2,共有的性质是( )
| A、开口向下 |
| B、对称轴是y轴 |
| C、都有最低点 |
| D、y随x的增大而减小 |
 (1)在边长为1的正方形网格中,以AB为边作一个正方形.
(1)在边长为1的正方形网格中,以AB为边作一个正方形.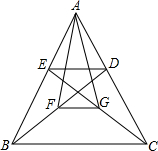 如图所示,一个△ABC,D是AC边上的一点,E是AB边上的一点,F是线段BD的中点,G是线段CE的中点,求△AFG的面积和四边形BCDE的面积比.
如图所示,一个△ABC,D是AC边上的一点,E是AB边上的一点,F是线段BD的中点,G是线段CE的中点,求△AFG的面积和四边形BCDE的面积比.