题目内容
20．已知关于x的一元二次方程mx2-4x-6=0的两根为x1和x2，且x1+x2=-2，则m=-2；（x1+x2）${\;}^{{x}_{1}•{x}_{2}}$=-8．分析 首先根据两根之和求得m的值，然后求得两根之积，最后求得代数式的值即可．
解答 解：∵关于x的一元二次方程mx2-4x-6=0的两根为x1和x2，且x1+x2=-2，
∴x1+x2=$\frac{4}{m}$=-2
解得：m=-2，
∴x1•x2=$\frac{-6}{-2}$=3
∴（x1+x2）x1•x2=（-2）3=-8．
故答案为：-2，-8．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
请在如图4×4方格中画一个边长为$\sqrt{10}$的正方形，要求正方形的顶点在格点上．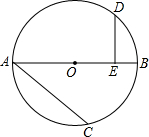
如图，已知AB为⊙O的直径，D、C为⊙O上两点，弧AD=弧DC，连结AC．过点D作DE⊥0B于E．求证：DE=$\frac{1}{2}$AC．
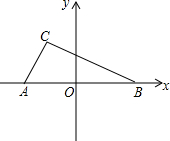在△ABC中，∠ACB=90°，∠BAC=60°，AC=2，如图，以AB所在的直线为x轴，以AB的垂直平分线为y轴，建立直角坐标系，求点A、B、C的坐标．