题目内容
已知，△ABC内接于⊙O，点P是圆外一点且OA垂直PA于点A，OB垂直PB于B，若∠C=62°，求∠APB的度数．（画出图形并写清必要的解题步骤）
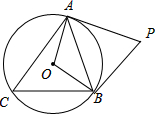解：如图，∵∠C=62°，∴∠AOB=2∠C=124°，
∵OA垂直PA于点A，OB垂直PB于B，
∴∠PAO=∠PBO=90°，
∴∠APB=360°-∠AOB-∠PAO-∠PBO=56°．
分析：首先根据题意画出图形，然后由圆周角定理，求得∠AOB的度数，又由OA垂直PA于点A，OB垂直PB于B，根据四边形的内角和定理，即可求得∠APB的度数．
点评：此题考查了圆周角定理以及四边形的内角和定理．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
25、附加题：如图所示，已知，△ABC内接于⊙O，AB为直径，∠CAE=∠B．
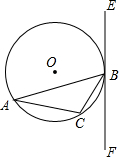已知：△ABC内接于⊙O，过点B作直线EF，AB为非直径的弦，且∠CBF=∠A．
（2013•南开区一模）如图，已知：△ABC内接于⊙O，点D在OC的延长线上，∠B=∠D=30°．