题目内容
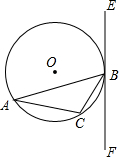 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.(1)求证:EF是⊙O的切线;
(2)若∠A=30°,BC=2,连接OC并延长交EF于点M,求由弧BC、线段BM和CM所围成的图形的面积.
分析:(1)连接BO并延长交⊙O于H,连接HC,首先根据圆周角定理得到∠H=∠A,由HB是直径得到∠HCB=90°,即∠H+∠CBH=90°,然后利用已知条件得到∠CBF+∠CBH=90°,即HB⊥EF,由此即可证明题目结论;
(2)在Rt△HCB中由BC=2,∠H=∠A=30°得到HB=4,OB=2,又∠BOM=2∠A=60°,根据三角函数可以求出MB,而
S=S△OBM-S扇形OBC=
OB•BM-
,由此即可求出由弧BC、线段BM和CM所围成的图形的面积.
(2)在Rt△HCB中由BC=2,∠H=∠A=30°得到HB=4,OB=2,又∠BOM=2∠A=60°,根据三角函数可以求出MB,而
S=S△OBM-S扇形OBC=
| 1 |
| 2 |
| 60π×22 |
| 360 |
解答: (1)证明:连接BO并延长交⊙O于H,连接HC,
(1)证明:连接BO并延长交⊙O于H,连接HC,
则∠H=∠A,∵HB是直径,∴∠HCB=90°
∴∠H+∠CBH=90°.
又∵∠A=∠CBF
∴∠CBF+∠CBH=90°
∴HB⊥EF.
又∵OB是半径,
∴EF是⊙O的切线.
(2)解:在Rt△HCB中,BC=2,∠H=∠A=30°,
∴HB=4,OB=2.
∵∠BOM=2∠A=60°,
∴BM=OB×tan60°=2
,
S=S△OBM-S扇形OBC=
OB•BM-
=
×2×2
-
=2
-
.
∴由弧BC、线段BM和CM所围成的图形的面积为2
-
.
 (1)证明:连接BO并延长交⊙O于H,连接HC,
(1)证明:连接BO并延长交⊙O于H,连接HC,则∠H=∠A,∵HB是直径,∴∠HCB=90°
∴∠H+∠CBH=90°.
又∵∠A=∠CBF
∴∠CBF+∠CBH=90°
∴HB⊥EF.
又∵OB是半径,
∴EF是⊙O的切线.
(2)解:在Rt△HCB中,BC=2,∠H=∠A=30°,

∴HB=4,OB=2.
∵∠BOM=2∠A=60°,
∴BM=OB×tan60°=2
| 3 |
S=S△OBM-S扇形OBC=
| 1 |
| 2 |
| 60π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
∴由弧BC、线段BM和CM所围成的图形的面积为2
| 3 |
| 2π |
| 3 |
点评:此题主要考查了切线的性质与判定,首先利用切线的判定定理判定切线,然后利用切线的性质和三角函数的定义即可求解.

练习册系列答案
相关题目
 25、附加题:如图所示,已知,△ABC内接于⊙O,AB为直径,∠CAE=∠B.
25、附加题:如图所示,已知,△ABC内接于⊙O,AB为直径,∠CAE=∠B. (2013•南开区一模)如图,已知:△ABC内接于⊙O,点D在OC的延长线上,∠B=∠D=30°.
(2013•南开区一模)如图,已知:△ABC内接于⊙O,点D在OC的延长线上,∠B=∠D=30°.