题目内容
已知锐角△ABC内接于圆O，作△ABC的BC边上的高，CA边上的中线，∠C的平分线并延长，分别交圆O于A′、B′、C′．
求证：S△ABC≤S△A'BC+S△AB'C+S△ABC′．
求证：S△ABC≤S△A'BC+S△AB'C+S△ABC′．
分析：首先设△ABC中，CA，AB上的高的延线分别交△ABC外接圆于B″、C″，垂心为P，利用垂心的性质，可得
S△ABC=S△A′BC+S△AB″C+S△ABC″，在分别设P为外心，重心，内心，则可得：S△ABC≤S△A'BC+S△AB'C+S△ABC'．
S△ABC=S△A′BC+S△AB″C+S△ABC″，在分别设P为外心，重心，内心，则可得：S△ABC≤S△A'BC+S△AB'C+S△ABC'．
解答：证明：如图所示，
①
设△ABC中，CA，AB上的高的延线分别交△ABC外接圆于B1、C1，
则P为△ABC的垂心，则有S△ABC=S△A′BC+S△AB1C+S△ABC1，
②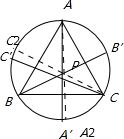
设△ABC中，BC，AB上的中线的延线分别交△ABC外接圆于A2、C2，
若P为△ABC的重心，则有 S△ABC≤S△A2BC+S△AB′C+S△ABC2，
③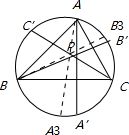
设△ABC中，∠ABC，∠CAB上的中线的延线分别交△ABC外接圆于B3、A3，
若P为△ABC的内心，则有 S△ABC≤S△A3BC+S△AB′3C+S△ABC′，当且仅当△ABC为正三角形时等号成立．
∴S△ABC≤S△A'BC+S△AB'C+S△ABC'．
①
设△ABC中，CA，AB上的高的延线分别交△ABC外接圆于B1、C1，
则P为△ABC的垂心，则有S△ABC=S△A′BC+S△AB1C+S△ABC1，
②
设△ABC中，BC，AB上的中线的延线分别交△ABC外接圆于A2、C2，
若P为△ABC的重心，则有 S△ABC≤S△A2BC+S△AB′C+S△ABC2，
③
设△ABC中，∠ABC，∠CAB上的中线的延线分别交△ABC外接圆于B3、A3，
若P为△ABC的内心，则有 S△ABC≤S△A3BC+S△AB′3C+S△ABC′，当且仅当△ABC为正三角形时等号成立．
∴S△ABC≤S△A'BC+S△AB'C+S△ABC'．
点评：此题考查了三角形的内心与垂心以及重心的性质．解此题的关键是注意三角形“四心”与一组面积公式的应用．
练习册系列答案
相关题目
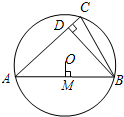如图，已知⊙O的半径为1，锐角△ABC内接于⊙O，BD⊥AC于点D，OM⊥AB于点M，则sin∠CBD的值等于（ ）| A、OM的长 | B、2OM的长 | C、CD的长 | D、2CD的长 |
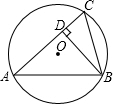如图，已知⊙O的半径为5，锐角△ABC内接于⊙O，BD⊥AC于点D，AB=8，则tan∠CBD的值等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
如图，已知⊙O的半径为
已知：如图，锐角△ABC内接于⊙O，∠ABC=45°；点D是