题目内容
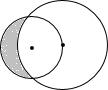
 如图所示,一个半径为R,重为G的均匀圆柱体,现在其边缘上作用一拉力,使它能滚上高为h的台阶,则拉力应作用于哪一点沿哪个方向才能最省力?最小拉力为多大?
如图所示,一个半径为R,重为G的均匀圆柱体,现在其边缘上作用一拉力,使它能滚上高为h的台阶,则拉力应作用于哪一点沿哪个方向才能最省力?最小拉力为多大?
分析:本题中支点是A,当拉力的作用点是过A点的直径的另一端点.过圆心O作底面的垂线OG,过A作AC⊥OG与点C.根据勾股定理就可以求出AC的长,再根据杠杆平衡条件求出力的大小.
解答: 解:如图所示,
解:如图所示,
使圆柱体滚上台阶,拉力最小时,力臂应最长,即为圆柱体的直径AB=2R,
方向垂直于过A点的直径斜向上,那么重力的力臂为AC,
由AC=
=
=
,
再由杠杆平衡条件,得F•2R=G•AC,
∴F=
.
答:拉力应作用在垂直于地A点的直径斜向上,最小拉力为F=
.
 解:如图所示,
解:如图所示,使圆柱体滚上台阶,拉力最小时,力臂应最长,即为圆柱体的直径AB=2R,
方向垂直于过A点的直径斜向上,那么重力的力臂为AC,
由AC=
| OA2-OC2 |
| R2-(R-h)2 |
=
| 2Rh-h2 |
再由杠杆平衡条件,得F•2R=G•AC,
∴F=
| G |
| 2R |
| 2Rh-h2 |
答:拉力应作用在垂直于地A点的直径斜向上,最小拉力为F=
| G |
| 2R |
| 2Rh-h2 |
点评:本题主要考查了勾股定理,是数学知识在实际生活中的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,一个半径为
如图所示,一个半径为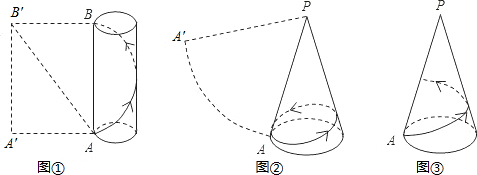
 如图所示,一个半径为
如图所示,一个半径为 如图所示,一个半径为3cm,弧长为πcm的扇形,让弧
如图所示,一个半径为3cm,弧长为πcm的扇形,让弧