Question

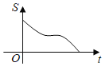
【题目】如图，在△ABC中，∠B＝135°，端点为A的射线l∥CB，点A绕射线l上的某点D旋转一周所形成的图形为F，点B在图形F上．

（1）利用尺规作图确定点D的位置；

（2）判断直线BC与图形F的公共点个数，并说明理由；

（3）若AD＝2，∠C＝15°，求直线AC被图形F所截得的线段的长．

Answer 1

【答案】（1）详见解析；（2）直线BC与图形F的公共点个数为1个，理由详见解析；（3）．

【解析】

（1）作线段AB的垂直平分线交直线l于点D，点D即为所求．

（2）直线BC与图形F的公共点个数为1个．证明DB⊥BC即可解决问题．

（3）设直线AC交⊙D于E，连接BE，作BH⊥AE于H．解直角三角形求出AH，HE即可解决问题．

解：（1）如图，点D即为所求．

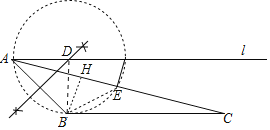
（2）直线BC与图形F的公共点个数为1个．

理由：∵直线l∥BC，

∴∠DAB+∠ABC＝180°，

∵∠ABC＝135°，

∴∠DAB＝45°，

∵DA＝DB，

∴∠DAB＝∠DBA＝45°，

∴∠ADB＝90°，

∵∠DBC＝∠ADB，

∴∠DBC＝90°，

∴DB⊥BC，

∴直线BC是⊙D的切线，

∴直线BC与图形F的公共点个数为1个．

（3）设直线AC交⊙D于E，连接BE，作BH⊥AE于H．

∵AD∥BC，

∴∠DAC＝∠C＝15°，

∵∠DAB＝45°，

∴∠BAC＝45°﹣15°＝30°，

∵AD＝DB＝2，

∴AB＝AD＝2，

∴BH＝AB＝，AH＝BH＝，

∵∠AEB＝∠ADB＝45°，∠BHE＝90°，

∴EH＝BH＝，

∴AE＝AH+BH＝．