题目内容
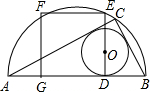
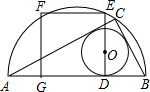
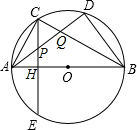
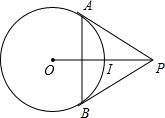
如图,PA、PB分别切⊙O于A、B两点,连接AB和OP,OP交⊙O于点I,则I是△PAB的( )
| A.内心 | B.外心 |
| C.三条高的交点 | D.三边上的中线的交点 |

∵PA、PB分别切⊙O于A、B两点,
∴PA=PB,∠OPA=∠OPB,
∴PI平分∠APB,PO⊥AB,
∴
=
,
∵∠PAI=
AOI,∠BAI=
∠AOI,
∴∠PAI=∠IAB,
∴AI是∠PAB的平分线,
∴I是两条角平分线的交点,
∴I是△PAB的内心.
故选:A.

∴PA=PB,∠OPA=∠OPB,
∴PI平分∠APB,PO⊥AB,
∴
 |
| AI |
 |
| BI |
∵∠PAI=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PAI=∠IAB,
∴AI是∠PAB的平分线,
∴I是两条角平分线的交点,
∴I是△PAB的内心.
故选:A.


练习册系列答案
相关题目