题目内容
1.已知如图所示,BC为半圆O的直径,AB⊥BC,垂足为D,过点B作弦BF交AD于点E,交半圆O于点F,弦AC与BF交于点H,且AE=BE,求证:(1)![]() =
=![]() ;(2)AH·BC=2AB·BE.
;(2)AH·BC=2AB·BE.

2.在上题中若加上条件sin∠FBC=![]() ,AB=4
,AB=4![]() ,求AD的长.
,求AD的长.
答案:
解析:
提示:
解析:
|
1.解答:(1)∵AE=BE,∴∠BAE=∠ABE. 而∠BAE=∠ACB,∠ACB=∠ABE=∠ACF,∴∠ACB=∠FCA,即 (2)如图,延长BA与CF延长线交于M.∵BC是直径,∴∠BAC= ∴∠EAH=∠AHE=∠ABC=∠BMC. ∴△AEH∽△BCM,∴ 而AE=BE,即AH·BC=2AB·BE. 2.解答:设DE=3x,∴sin∠FBC= 在Rt△ABD中,则(8x)2+(4x)2=(4 解得x=1,∴AD=8. |
提示:
|
1.名师导引:(1)∠ACB=∠BAD,而AE=BE,∴∠ABE=∠BAE,∠FCA=∠ABE. (2)延长BA与CF延长线交于M.证明△AEH∽△BMC. 2.名师导引:令DE=3x,则BE=5x,BD=4x,构建直角三角形求出x. 点评:运用三角函数,勾股定理是求线段常见方法. |

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目

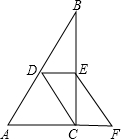 已知如图所示,D,E分别为AB,BC的中点,CD=
已知如图所示,D,E分别为AB,BC的中点,CD= (2011•巴中)已知如图所示,在平面直角坐标系中,四边形ABC0为梯形,BC∥A0,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,O).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒.
(2011•巴中)已知如图所示,在平面直角坐标系中,四边形ABC0为梯形,BC∥A0,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,O).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒. 是劣弧
是劣弧 的2倍;⑤AE=BC.其中正确结论的有_____个.
的2倍;⑤AE=BC.其中正确结论的有_____个.

