Question

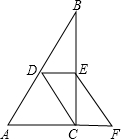已知如图所示，D，E分别为AB，BC的中点，CD=

1

2

AB，点F在AC的延长线上，∠FEC=∠B．求证：CF=DE．

Answer 1

分析：根据三角形的中位线定理可知，DE∥AC，DE=

1

2

AC．再利用平行四边形的性质解答即可．

解答：证明：∵D，E分别为AB，BC的中点，
∴DE∥AC，DE=

1

2

AC．
又∵CD=

1

2

AB=DB，
∴∠B=∠BCD．
∵∠FEC=∠B，
∴∠FEC=∠BCD．
∴EF∥DC．
∴四边形DCFE是平行四边形．
∴CF=DE．

点评：本题考查了平行四边形的判定和三角形的中位线定理，三角形的中位线的性质定理，为证明线段相等和平行提供了依据．