题目内容
12．
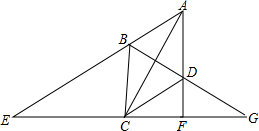如图．菱形ABCD，AE=3AF，求证：BG=3DG．
分析 由CD∥AE知△CDF∽△EAF，从而得出$\frac{AF}{AE}=\frac{DF}{DC}=\frac{1}{3}$，根据BC=CD得$\frac{DF}{BC}=\frac{1}{3}$，再由BC∥DF知△DFG∽△BCG，即可得$\frac{DF}{BC}=\frac{DG}{BG}=\frac{1}{3}$，从而得证．
解答 证明：∵四边形ABCD是菱形，
∴CD∥AE，
∴△CDF∽△EAF，
∵AE=3AF，
∴$\frac{AF}{AE}=\frac{DF}{DC}=\frac{1}{3}$，
∵BC=CD，
∴$\frac{DF}{BC}=\frac{1}{3}$，
又∵BC∥DF，
∴△DFG∽△BCG，
∴$\frac{DF}{BC}=\frac{DG}{BG}=\frac{1}{3}$，
∴BG=3DG．
点评 本题主要考查相似三角形的判定与性质及菱形的性质，熟练掌握预备定理是解题的关键．
练习册系列答案
相关题目
17．
为了解某县2014年初中毕业生的实验成绩等级的分布情况，随机抽取了该县若干名学生的实验成绩进行统计分析，并根据抽取的成绩绘制了如图所示的统计图表：
请根据以上统计图表提供的信息，解答下列问题：
（1）本次抽查的学生有200名；
（2）表中x，y和m所表示的数分别为：x=100，y=30，m=5%；
（3）请补全条形统计图；
（4）若将抽取的若干名学生的实验成绩绘制成扇形统计图，则实验成绩为D类的扇形所对应的圆心角的度数是多少．
为了解某县2014年初中毕业生的实验成绩等级的分布情况，随机抽取了该县若干名学生的实验成绩进行统计分析，并根据抽取的成绩绘制了如图所示的统计图表：请根据以上统计图表提供的信息，解答下列问题：
（1）本次抽查的学生有200名；
（2）表中x，y和m所表示的数分别为：x=100，y=30，m=5%；
（3）请补全条形统计图；
| 成绩等级 | A | B | C | D |
| 人数 | 60 | x | y | 10 |
| 百分比 | 30% | 50% | 15% | m |
如图，直角△ABC中，AB=5，BC=3，AC=4，直角△ABC将沿着它的一条边AB旋转一周，得到一个什么图形？试求出其表面积和点C运动的路程．
已知在纸面上有一数轴（如图），折叠纸面．例如：若数轴上数2表示的点与数-2表示的点重合，则数轴上数-4表示的点与数4表示的点重合，根据你对例题的理解，解答下列问题：