题目内容
6.下列说法错误的是( )| A. | 若$\frac{x}{a}$=$\frac{y}{a}$,则x=y | B. | 若x2=y2,则-4ax2=-4ay2 | ||
| C. | 若a=b,则$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$ | D. | 如果(a+1)x=a+1,那么x=1 |
分析 根据等式的性质进行逐一分析判断.
解答 解:A、根据等式的性质(2),即等式的两边同乘以a(不为0),则等式仍然成立,不符合题意;
B、根据等式的性质(2),即等式的两边同乘以-4a,则等式仍然成立,不符合题意;
C、根据等式的性质(2),即等式的两边同除以c2+1,则等式仍然成立,不符合题意;
D、根据等式的性质(2),当a+1=0时,等式不成立,符合题意.
故选D.
点评 本题主要考查了等式的基本性质.等式性质:1、等式的两边同时加上或减去同一个数或字母,等式仍成立;2、等式的两边同时乘以或除以同一个不为0数或字母,等式仍成立.

练习册系列答案
相关题目
17.下列各组数中,互为相反数的是( )
| A. | -(+7)和+(-7) | B. | -(-7)与7 | C. | -|-1$\frac{1}{5}$|与-(-$\frac{6}{5}$) | D. | +(-$\frac{1}{100}$)与+(-0.01) |
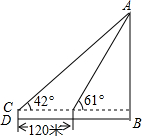 如图,为了测得电视塔的高度AB,在D处用高为1.2米的测角仪CD,测得电视塔顶端A的仰角为42°,再向电视塔方向前进120米,又测得电视塔顶端A的仰角为61°,求这个电视塔的高度AB.(精确到1米)
如图,为了测得电视塔的高度AB,在D处用高为1.2米的测角仪CD,测得电视塔顶端A的仰角为42°,再向电视塔方向前进120米,又测得电视塔顶端A的仰角为61°,求这个电视塔的高度AB.(精确到1米)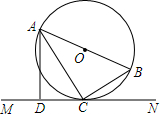 如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.
如图,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且AC平分∠BAD.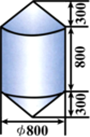 锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)
锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆锥,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀100个这样的锚标浮筒需要用多少锌?(π取3.14,精确到0.1kg)