题目内容
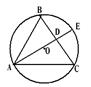
如图,在△ABC中,AB=4,AC=6,∠BAC=60º,∠BAC的角平分线交△ABC的外接圆⊙O于点E,则AE的长为 .

 或
或
试题分析:

过B作BF⊥AC于点F。在Rt△BAF中,∵∠BAF=60°,
所以AF=
 AB=2.BF=
AB=2.BF= ,则CF=AC-AF=6-2=4
,则CF=AC-AF=6-2=4所以

连结BO交圆O于点M。连结MC、OC。

根据同弧所对圆周角相等,可知:∠BMC=∠BAC=60°。
则sin∠BMC=sin∠BAC=
 。即
。即
又因为△MOC为等腰三角形。所以△MOC是等边三角形。
则MC=OM=OC=r=


过E点作EC⊥AC于点H。设AE=x,则EH=
 x。AH=
x。AH= x。CH=6-
x。CH=6- x。
x。所以

解得x1=
 ,x2=
,x2= 则AE=
则AE= 或
或 。
。点评:本题难度较大。主要考查学生对圆及三角函数知识点的综合运用,一般为压轴题型,要求学生多做训练,注意 数形结合思想的培养,运用到考试中去。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 ∠BOD,则⊙O的半径为
∠BOD,则⊙O的半径为



 分别交OA,OB于点M,N.
分别交OA,OB于点M,N.
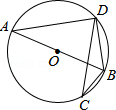
 的中点,连接PA,PB,PC.
的中点,连接PA,PB,PC. 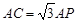 ;
;
 ,求
,求 的值.
的值.