Question

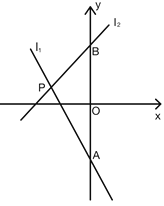
【题目】如图，已知直线，直线，与相交于点，，分别与轴相交于点.

(1)求点P的坐标.

(2)若，求x的取值范围.

(3)点为x轴上的一个动点，过作x轴的垂线分别交和于点，当EF=3时，求m的值.

Answer 1

【答案】(1)P(-2，1)；(2)-3<x<-2；(3)m=-3或m=-1.

【解析】

（1）由点P是两直线的交点，则由两方程的函数值相等，解出x，即可得到点P坐标；

（2）由，联立成不等式组，解不等式组即可得到x的取值范围；

（3）由点D的横坐标为m，结合EF=3，可分为两种情况进行讨论：点D在点P的左边；点D在点P的右边，分别计算，即可得到m的值.

解：(1)P点是直线l1与直线l2的交点，可得：2x3=x+3，

解得：x=2 ，

∴y=1；

∴ P点的坐标为：(2，1)；

(3)，

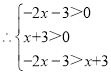，解得：；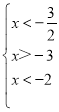

；

(3)∵点D为(m，0)，根据题意可知，

则E(m，2m3)；F(m，m+3)，

第一种情况：点D在点P的左边时，此时点E在点F的上方；

∴，

；

第二种情况：点D在点P的右边时，此时点E在点F的下方；

∴，

；

∴m的值为：或.