��Ŀ����
6��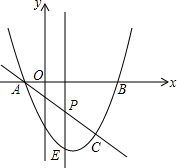 ��ͼ��������y=x2-2x-3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��ֱ��y=kx+b�������߽���A��C���㣬����C��ĺ�����Ϊ2��
��ͼ��������y=x2-2x-3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ��ֱ��y=kx+b�������߽���A��C���㣬����C��ĺ�����Ϊ2����1����ֱ��AC�ĺ�������ʽ��
��2��P���߶�AC�ϵ�һ�����㣬��P��y���ƽ��˼�����������ڵ�E�����ACE��������ֵ��
��3����G���������ϵĶ��㣬��x�����Ƿ���ڵ�F��ʹA��C��F��GΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����������������F�����ꣻ����˵�����ɣ�
���� ��1����Ϊ��������x���ཻ�����Կ���y=0�����A��B�����꣮�ٸ���C�����������ϣ�C��ĺ�����Ϊ2�������������м��ɵó�C������꣮�ٸ�������ʽ���̼��ɽ��AC�ĺ�������ʽ��
��2������P����AC�Ͽ����P������꣮E������ɸ�����֪����������ã���ΪPE���ڴ�ֱ��x���ֱ���ϣ���������֮��ľ���Ϊ|xA-xC|�г����̺��϶��κ��������ʼ��ɵó��𰸣�
��3�������ĸ������ĵ㣮
������C�������ߺ�y��Ľ��㣬��ôCG��x�ᣬ��ʱAF=CG=2�����F��������ǣ�-3��0����
��AF=CG=2��A���������-1��0�������F���������1��0����
�۴�ʱC��G��������������x��Գƣ����G���������Ϊ3�������������м��ɵó�G�������Ϊ��1+$\sqrt{7}$��3��������ֱ��GF��AC����ͬ����˿���ֱ��GF�Ľ���ʽΪy=-x+h����G������ɵó�ֱ�ߵĽ���ʽΪy=-x+7�����ֱ��GF��x��Ľ���F������Ϊ��4+$\sqrt{7}$��0������ͬ�ۿ����F������Ϊ��4-$\sqrt{7}$��0����
�ۺ���������ɵó�������4������������F�㣮
��� �⣨1����y=0ʱ�����x1=-1��x2=3��
��A��-1��0��B��3��0����
��C������x=2����y=x2-2x-3��y=-3��
��C��2��-3����
��ֱ��AC�Ľ���ʽΪy=kx+b������A�͵�C���������ã�
$\left\{\begin{array}{l}{-k+b=0}\\{2k+b=-3}\end{array}\right.$��
��ã�k=-1��b=-1��
��ֱ��AC�ĺ�������ʽ��y=-x-1��
��2����P��ĺ�����Ϊx��-1��x��2����
��P��E������ֱ�ΪP��x��-x-1����E��x��x2-2x-3����
��P����E����Ϸ���PE=��-x-1��-��x2-2x-3��=-x2+x+2��
��S��ACE=$\frac{1}{2}$PE��|xA-xC|=$\frac{1}{2}$��-x2+x+2����3=-$\frac{3}{2}$x2+$\frac{3}{2}$x+3��
��S��ACE=-$\frac{3}{2}$��x-$\frac{1}{2}$��2+$\frac{27}{8}$
��x=$\frac{1}{2}$ʱ��S��ACE���Ϊ$\frac{27}{8}$��
��3������4�������ĵ�F���ֱ���F1��1��0����F2��-3��0����F3��4+$\sqrt{7}$��0����F4��4-$\sqrt{7}$��0����
����ͼ1������C�������ߺ�y��Ľ��㣬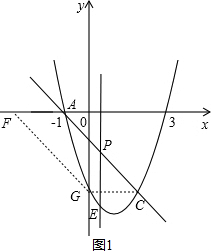
��C��2��-3����G��0��-3��
��CG��x�ᣬ��ʱAF=CG=2��
��F��������ǣ�-3��0����
����ͼ2��AF=CG=2��A�������Ϊ��-1��0�������F�������Ϊ��1��0����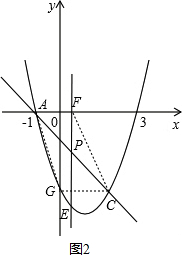
����ͼ3����ʱC��G��������������x��Գƣ����G���������Ϊ3�������������м��ɵó�G�������Ϊ��1��$\sqrt{7}$��3��������ֱ��GF��AC����˿���ֱ��GF�Ľ���ʽΪy=-x+h����G������ɵó�ֱ�ߵĽ���ʽΪy=-x+4+$\sqrt{7}$�����ֱ��GF��x��Ľ���F������Ϊ��4+$\sqrt{7}$��0����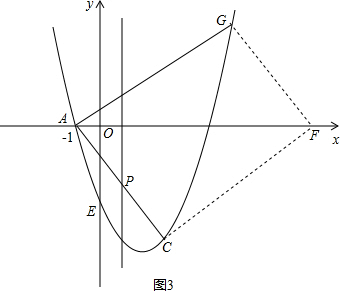
����ͼ4��ͬ�ۿ����F������Ϊ��4-$\sqrt{7}$��0����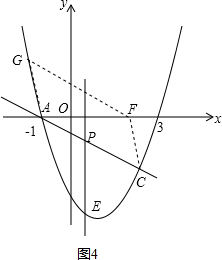
�ۺ���������ɵó�������4������������F�㣮
���� ������Ҫ�����˶��κ������ۺ��⣬�漰���˴���ϵ������һ�κ�������ʽ��ƽ���ı��ε��ж������κ��������ʵ���Ҫ֪ʶ�㣬�ۺ���ǿ�������Ĺؼ���Ҫ��ѧ�����շ������ۣ����ν�ϵ���ѧ˼�뷽����������һ�����Ѷȣ�

 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д� ��ͼ���������ϣ���P��Ӧ��ʵ���ǣ�������
��ͼ���������ϣ���P��Ӧ��ʵ���ǣ�������| A�� | $\sqrt{2}$ | B�� | $\sqrt{5}$ | C�� | �� | D�� | -1.5 |
| A�� | |x| | B�� | $\frac{1}{|x|}$ | C�� | -|x| | D�� | -$\frac{1}{|x|}$ |
 ��ͼֱ��l1��l2��һ�麬45��ǵ�ֱ�����ǰ���ͼ��ʾ���ã���1=60�㣬���2=105�㣮
��ͼֱ��l1��l2��һ�麬45��ǵ�ֱ�����ǰ���ͼ��ʾ���ã���1=60�㣬���2=105�㣮