题目内容
10. 如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,AB=4,CE=1,求⊙O半径长.
如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,AB=4,CE=1,求⊙O半径长.
分析 连接OA,由垂径定理可知AE=$\frac{1}{2}$AB=2,OE=OC-CE=r-1,OA=r,在Rt△AOE中,利用勾股定理求r即可.
解答 解:连接OA, 如图所示:
如图所示:
设⊙O半径长为r,
∵CD⊥AB,
∴AE=$\frac{1}{2}$AB=2,
又∵OE=OC-CE=r-1,OA=r,
在Rt△AOE中,由勾股定理得:AE2+OE2=OA2,
即22+(r-1)2=r2,
解得r=2.5,
即⊙O半径长为2.5.
点评 本题考查了垂径定理,勾股定理的运用.连接半径,将问题转化到直角三角形中,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
20.已知二次函数的解析式为y=(x-2)2+1,则该二次函数图象的顶点坐标是 ( )
| A. | (-2,1) | B. | (2,1) | C. | (2,-1) | D. | (1,2) |
2.若※是新规定的运算符号,设a※b=a2-ab,则3※12的值是( )
| A. | -6 | B. | -3 | C. | 15 | D. | -27 |
20. 如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
 如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )
如图,反比例函数y=-$\frac{2}{x}$的图象上有一点A,过点A作AB⊥x轴于B,则S△AOB是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
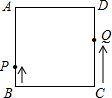 已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s)
已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s)