题目内容
 如图,在Rt△OAB中,∠OBA=90°,点B在x轴上,点A在第二象限,已知双曲线y=
如图,在Rt△OAB中,∠OBA=90°,点B在x轴上,点A在第二象限,已知双曲线y=| k | x |
(-3,2)
(-3,2)
;(2)△AOC的面积为9
9
.分析:(1)直接根据点D是OA的中点即可求出D点坐标;
(2)由(1)中D点坐标即可求出反比例函数的解析式,故可得出△OBC的面积,由S△AOC=S△AOB-S△OBC即可得出结论.
(2)由(1)中D点坐标即可求出反比例函数的解析式,故可得出△OBC的面积,由S△AOC=S△AOB-S△OBC即可得出结论.
解答:解:(1)∵D是OA的中点,点A的坐标为(-6,4),
∴D(
,
),即(-3,2),
故答案为:(-3,2);
(2)∵D(-3,2)在反比例函数y=
的图象上,
∴k=(-3)×2=-6,
∴S△OBC=
×6=3,
∴S△AOC=S△AOB-S△OBC=
×6×4-3=9.
故答案为:9.
∴D(
| -6 |
| 2 |
| 4 |
| 2 |
故答案为:(-3,2);
(2)∵D(-3,2)在反比例函数y=
| k |
| x |
∴k=(-3)×2=-6,
∴S△OBC=
| 1 |
| 2 |
∴S△AOC=S△AOB-S△OBC=
| 1 |
| 2 |
故答案为:9.
点评:本题考查的是反比例函数综合题,熟知反比例函数中k=xy的特点是解答此题的关键.

练习册系列答案
相关题目
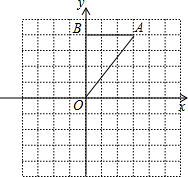 如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).
如图,在Rt△OAB中,∠OBA=90°,且点B的坐标为(0,4).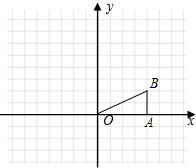 OA1B1.
OA1B1.
 如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
如图,在Rt△OAB中,∠OBA=90°,OB=AB=4,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1. (2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.
(2009•株洲)如图,在Rt△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O沿逆时针方向旋转90°得到△OA1B1.