题目内容
15. 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由C为弧EB中点,利用垂径定理的逆定理得到OC垂直于BE,根据等弧对等弦得到BC=EC,再由AB为直角,利用圆周角定理得到AE垂直于BE,进而得到一对直角相等,利用同位角相等两直线平行得到OC与AE平行,由AD为圆的切线,利用切线的性质得到AB与DA垂直,利用同角的余角相等得到∠DAE=∠ABE,根据E不一定为弧AC中点,可得出AC与OE不一定垂直,即可确定出结论成立的序号.
解答 解:∵C为$\widehat{EB}$的中点,即$\widehat{BC}=\widehat{CE}$,
∴OC⊥BE,BC=EC,选项②正确;
∴∠BFO=90°,
∵AB为圆O的直径,
∴AE⊥BE,即∠BEA=90°,
∴∠BFO=∠BEA,
∴OC∥AE,选项①正确;
∵AD为圆的切线,
∴∠DAB=90°,即∠DAE+∠EAB=90°,
∵∠EAB+∠ABE=90°,
∴∠DAE=∠ABE,选项③正确;
点E不一定为$\widehat{AC}$中点,故E不一定是$\widehat{AC}$中点,选项④错误,
则结论成立的是①②③,
故选C
点评 此题考查了切线的性质,圆周角定理,平行线的判定,以及垂径定理,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
3.在数轴上到原点的距离等于2的点所表示的数是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 不能确定 |
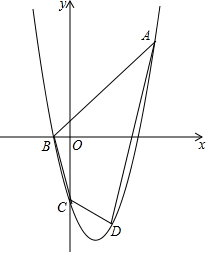 如图,抛物线y=ax2+bx-4(a≠0)经过点A(5,6),与x轴的负半轴交于点B,与y轴交于点C,且OC=4OB.
如图,抛物线y=ax2+bx-4(a≠0)经过点A(5,6),与x轴的负半轴交于点B,与y轴交于点C,且OC=4OB.
 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B'、C'处,联结BC'与AC边交于点D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B'、C'处,联结BC'与AC边交于点D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$. 如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.
如图,二次函数y=ax2+bx+c的最大值为$\frac{13}{6}$,其图象经过点A(0,-2)、B(5,-2),点C在x轴上,∠ACB=90°,且CA<CB,将△ABC饶点A逆时针旋转,使点C的对应点C′落在x轴上.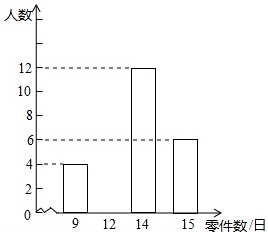 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题: 如图,在△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线交BC于D,若AD=6cm,则BC=9 cm.
如图,在△ABC中,∠C=90°,∠BAC=60°,∠BAC的平分线交BC于D,若AD=6cm,则BC=9 cm.