题目内容
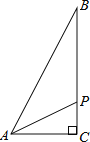
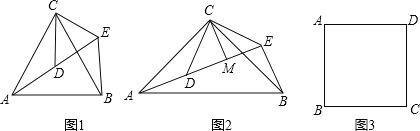
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上一点,且
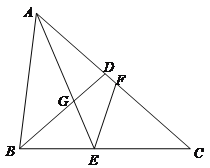
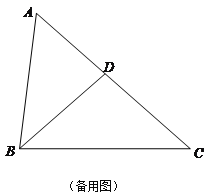
,D是AC边上一点,且![]() ,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),
,联结BD,点E、F分别是BC、AC上两点(点E不与B、C重合),![]() ,AE与BD相交于点G.
,AE与BD相交于点G.
(1)求证:BD平分![]() ;
;
(2)设![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)联结FG,当![]() 是等腰三角形时,求BE的长度.
是等腰三角形时,求BE的长度.
【答案】(1)证明见解析(2)![]() (3)
(3)![]() ,
,![]() ,
,![]()
【解析】分析:(1)依据![]() ,
,![]() ,即可得到
,即可得到![]() 的长,再根据
的长,再根据
![]() ,
,
即可得出![]() 的长,依据
的长,依据![]() 即可得到
即可得到![]() ,即
,即![]() 平分
平分![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,依据平行线分线段成比例定理以及相似三角形的对应边成比例,即可得到
,依据平行线分线段成比例定理以及相似三角形的对应边成比例,即可得到![]() ,进而得出
,进而得出![]() ,即可得到y与x之间的函数关系式;
,即可得到y与x之间的函数关系式;
(3)当![]() 是等腰三角形时,存在三种情况,分别依据相似三角形的对应边成比例,即可得到关于x的方程,进而得出BE的长.
是等腰三角形时,存在三种情况,分别依据相似三角形的对应边成比例,即可得到关于x的方程,进而得出BE的长.
详解(1)∵![]() ,又∵
,又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() 是公共角,
是公共角,
∴![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() ;
;
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,
∴
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() , 即
, 即![]()
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴![]() ;
;
(3)当△![]() 是等腰三角形时,存在以下三种情况:
是等腰三角形时,存在以下三种情况:
1° ![]() ,易证
,易证 ![]() ,即
,即![]() ,得到
,得到![]()
2° ![]() ,易证
,易证![]() ,即
,即![]() ,
,![]()
3° ![]() ,易证
,易证 ![]() ,即
,即![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目