题目内容
 如图,BE平分∠ABC,DE∥CB,AD=2,BC=4,求DE.
如图,BE平分∠ABC,DE∥CB,AD=2,BC=4,求DE.
解:∵BE平分∠ABC,DE∥CB,
∴∠DBE=∠EBC,∠EBC=∠DEB,
∴∠DBE=∠DEB,
∴DE=DB,
设DE=x,则DB=x,AB=2+x,
∵△ADE∽△ABC,
∴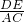 =
= ,即
,即 =
= ,
,
解得:x=2或-4(舍去),
故DE=2.
分析:根据BE平分∠ABC,DE∥CB,可判断出DE=DB,继而根据△ADE∽△ABC,利用相似三角形的性质可得出DE的长.
点评:此题考查了相似三角形的判定与性质及等腰三角形的判定与性质,解答本题的关键是根据题意判断出DE=DB,另外要熟练掌握相似三角形的性质.
∴∠DBE=∠EBC,∠EBC=∠DEB,
∴∠DBE=∠DEB,
∴DE=DB,
设DE=x,则DB=x,AB=2+x,
∵△ADE∽△ABC,
∴
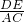 =
= ,即
,即 =
= ,
,解得:x=2或-4(舍去),
故DE=2.
分析:根据BE平分∠ABC,DE∥CB,可判断出DE=DB,继而根据△ADE∽△ABC,利用相似三角形的性质可得出DE的长.
点评:此题考查了相似三角形的判定与性质及等腰三角形的判定与性质,解答本题的关键是根据题意判断出DE=DB,另外要熟练掌握相似三角形的性质.

练习册系列答案
相关题目
 21、如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.
21、如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD. 10、如图,∵BE平分∠ABC(已知)
10、如图,∵BE平分∠ABC(已知) 如图,BE平分∠ABD,DE平分∠BDC,且BE⊥DE于E,那么AB∥CD吗?( )
如图,BE平分∠ABD,DE平分∠BDC,且BE⊥DE于E,那么AB∥CD吗?( ) 完成下面的证明:
完成下面的证明: 如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.
如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.