题目内容
我们知道:
1+2+3=
=6,1+2+3+4=
=10,那么1+2+3+…+100= .
1+2+3=
| 3×(3+1) |
| 2 |
| 4×(4+1) |
| 2 |
考点:有理数的加法
专题:规律型
分析:根据观察,可得连续自然数的求和公式:1+2+3+…+n=
,根据求和公式,可得答案.
| n(n+1) |
| 2 |
解答:解;1+2+3+…+100=
=5050,
故答案为:5050.
| 100×(1+100) |
| 2 |
故答案为:5050.
点评:本题考查了有理数的加法,利用了了连续自然数的求和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
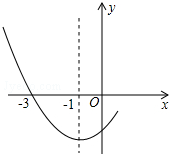 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(