题目内容
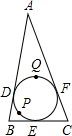如图，△ABC的内切圆分别切AB、BC、AC于D、E、F三点，其中P、Q两点分别在 |
| DE |
|
| DF |
|
| DPE |
|
| DQF |
分析：由于
、
所在的圆是同一个圆，因此半径相同，那么它们的弧长比应等于圆心角的度数比；设△ABC的内切圆为⊙O，连接OD、OE、OF，由切线的性质知OE⊥BC、OD⊥AB、OF⊥AC，由此可得∠DOE、∠B互补，∠DOF、∠A互补，由此求得两段弧的圆心角，即可得解．
|
| DPE |
|
| DQF |
解答：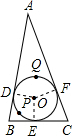
解：设△ABC的内切圆的圆心为O，连接OD、OE、OF；
则OD⊥AB，OE⊥BC，OF⊥AC；
∴∠ODB=∠OEB=∠ODA=∠OFA=90°，
∴∠DOE=180°-∠B=100°，∠DOF=180°-∠A=150°；
设⊙O的半径为R，则：
的长=
，
的长=
，
故
的长与
的长之比为：
．
故答案为：
．
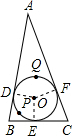解：设△ABC的内切圆的圆心为O，连接OD、OE、OF；则OD⊥AB，OE⊥BC，OF⊥AC；
∴∠ODB=∠OEB=∠ODA=∠OFA=90°，
∴∠DOE=180°-∠B=100°，∠DOF=180°-∠A=150°；
设⊙O的半径为R，则：
|
| DPE |
| 100×πR |
| 180 |
|
| DQF |
| 150×πR |
| 180 |
故
|
| DPE |
|
| DQF |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：此题主要考查了三角形的内切圆以及弧长的计算公式，难度不大．
练习册系列答案
相关题目
5、已知：如图，△ABC内接于⊙O，AE切⊙O于点A，BD∥AE交AC的延长线于点D，求证：AB2=AC•AD．
点E，连接AD、CE，若AC=7，AD=3
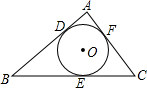已知如图，△ABC内切⊙O于D、E、F三点，内切圆⊙O的半径为1，∠C=60°，AB=5，则△ABC的周长为（ ）| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
内切于点B，BC是⊙O的直径，BC＝6，BF为
