题目内容
【题目】如图在平面直角坐标系中,点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
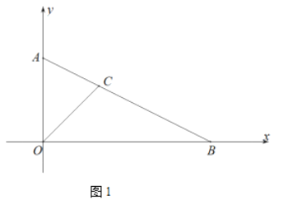
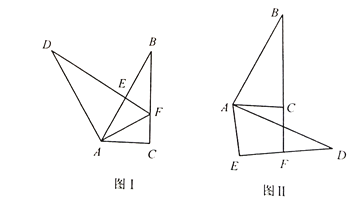
(1)如图1,求![]() 的长;
的长;
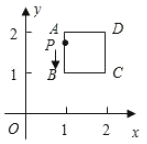
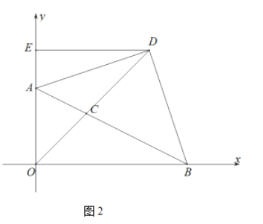
(2)如图2,![]() 是
是![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,若点
,若点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的关系;
的关系;
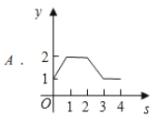
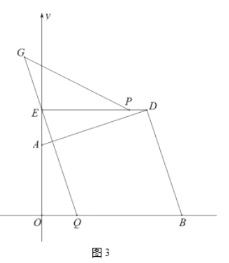
(3)在(2)的条件下,如图3,线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 值?
值?
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
![]()
【解析】
(1)作![]() 于
于![]() ,利用角平分线得到
,利用角平分线得到![]() 利用等角的三角函数值相等建立方程,再用勾股定理即可得到答案.
利用等角的三角函数值相等建立方程,再用勾股定理即可得到答案.
(2)过![]() 作
作![]() 于
于![]() ,证明
,证明![]() ,求解
,求解![]() 的长及
的长及![]() 的坐标,进而求解
的坐标,进而求解![]() 中
中![]() 上的高,利用面积公式可得答案,
上的高,利用面积公式可得答案,
(3)过![]() 作
作![]() 轴于
轴于![]() ,连接
,连接![]() 利用已知条件,结合相似三角形的性质证明四边形
利用已知条件,结合相似三角形的性质证明四边形![]() 为平行四边形,从而求解
为平行四边形,从而求解![]() 的长,过
的长,过![]() 作
作![]() 于
于![]() 利用
利用![]() 平行四边形的性质,等角的三角函数值相等建立方程,最后利用勾股定理可得答案.
平行四边形的性质,等角的三角函数值相等建立方程,最后利用勾股定理可得答案.
解:(1)如图,作![]() 于
于![]() ,
,
![]()
![]() 平分
平分![]() ,
,![]()
![]()
![]()
![]() 点
点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
解得:![]()
![]()
![]()

(2)如图,过![]() 作
作![]() 于
于![]() ,
,
![]() 平分
平分![]()
![]()
![]()
![]()
![]()
![]()
设![]() 则
则![]()
由![]()
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]()
![]()
![]()
![]()
![]()
![]()
由(1)知:![]()
![]()
![]()
![]()

(3)如图,过![]() 作
作![]() 轴于
轴于![]() ,连接
,连接![]()
由(2)知:![]() ,
,![]()
![]()
![]()
![]() 轴,
轴,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
由(2)知:![]()
![]()
由(2)得:![]() 轴,而
轴,而![]() ,
,
![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
过![]() 作
作![]() 于
于![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目