题目内容
18.点A(x1,y1),B(x2,y2)在正比例函数y=(-k+2)x的图象上,若(x1-x2)(y1-y2)<0,则k值可以是( )| A. | 2 | B. | -1 | C. | 1 | D. | 3 |
分析 根据异号得负判断出y随x的增大而减小,再根据正比例函数的性质列出不等式求出k的取值范围,然后判断即可.
解答 解:∵(x1-x2)(y1-y2)<0,
∴x1-x2<0时,y1-y2>0,
∴y随x的增大而减小,
∴-k+2<0,
解得k>2,
四个选项中只有k=3符合.
故选D.
点评 本题考查了一次函数图象上点的坐标特征,难点在于判断出一次函数的增减性,即y随x的增大而减小.

练习册系列答案
相关题目
8.单项式-32x2y3的系数和次数分别是( )
| A. | -3,5 | B. | 9,7 | C. | -9,7 | D. | -9,5 |
3.如果mn>0,且m+n<0,则下列选项正确的是( )
| A. | m>0,n<0 | B. | m<0,n<0 | ||
| C. | m、n异号,且负数的绝对值大 | D. | m、n异号,且正数的绝对值大 |
10.下列说法正确的是( )
| A. | 若a+b=0,则$\frac{a}{b}$=-1 | B. | 若|a|=-a,则a<0 | ||
| C. | 若a>b>0,则-a<-b<0 | D. | 若a<b<0,则$\frac{1}{a}$<$\frac{1}{b}$<0 |
7.计算$\frac{{a}^{2}b}{2ab}$结果正确的是( )
| A. | $\frac{2}{a}$ | B. | $\frac{a}{2}$ | C. | $\frac{b}{2a}$ | D. | 2a |
 如图,(单位:厘米),求半圆柱木料的表面积和体积.
如图,(单位:厘米),求半圆柱木料的表面积和体积.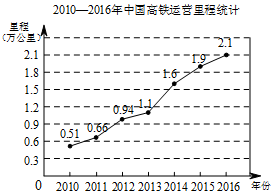 2016年我国高铁运营里程突破2万公里,占世界总里程的60%以上.如图,是我国2010-2016年高铁运营里程情况统计,根据统计图提供的信息,预估2017年我国高铁运营里程约为2.3万公里,你的预估理由是2016到2017年的增幅与2015到2016的增幅最相近.
2016年我国高铁运营里程突破2万公里,占世界总里程的60%以上.如图,是我国2010-2016年高铁运营里程情况统计,根据统计图提供的信息,预估2017年我国高铁运营里程约为2.3万公里,你的预估理由是2016到2017年的增幅与2015到2016的增幅最相近.