题目内容
9.幼儿园把新购进的一批玩具分给小朋友,若每人3件,那么还剩余59件;若每人5件,那么最后一个小朋友能分到玩具,但不足4件,共有小朋友31人,这批玩具共有152件.分析 本题可设共有x个小朋友,则玩具有3x+59个,令其<5(x-1)+4,令其≥5(x-1)+1,化解不等式组得出x的取值范围,则x即为其中的最小的整数.
解答 解:设共有x个小朋友,则玩具有3x+59个.
∵最后一个小朋友不足4件,
∴3x+59<5(x-1)+4,
∵最后一个小朋友最少1件,
∴3x+59≥5(x-1)+1,
联立得$\left\{\begin{array}{l}{3x+59<5(x-1)+4}\\{3x+59≥5(x-1)+1}\end{array}\right.$,
解得30<x≤31.5.
∵x取正整数31,
∴玩具数为3x+59=152.
故答案为:31,152.
点评 本题考查的是一元一次不等式的运用,要注意解不等式时不等号两边同时除以一个负数,不等式方向要改变.

练习册系列答案
相关题目
14.一个多边形的每一个外角都等于40°,则这个多边形的边数为( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
19.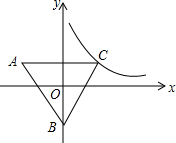 如图,等边△ABC的边长是2,内心O是直角坐标系的原点,点B在y轴上.若反比例函数y=$\frac{k}{x}$(x>0),则k的值是( )
如图,等边△ABC的边长是2,内心O是直角坐标系的原点,点B在y轴上.若反比例函数y=$\frac{k}{x}$(x>0),则k的值是( )
 如图,等边△ABC的边长是2,内心O是直角坐标系的原点,点B在y轴上.若反比例函数y=$\frac{k}{x}$(x>0),则k的值是( )
如图,等边△ABC的边长是2,内心O是直角坐标系的原点,点B在y轴上.若反比例函数y=$\frac{k}{x}$(x>0),则k的值是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |