题目内容
20. 如图,在等腰梯形ABCD中,AD∥BC,BC=4$\sqrt{3}$,AD=$\sqrt{3}$,∠B=30°,直角三角板含30°角的顶点E在边 BC上移动,一直角边始终经过点A,斜边与CD交于点F.设BE=x,CF=y.
如图,在等腰梯形ABCD中,AD∥BC,BC=4$\sqrt{3}$,AD=$\sqrt{3}$,∠B=30°,直角三角板含30°角的顶点E在边 BC上移动,一直角边始终经过点A,斜边与CD交于点F.设BE=x,CF=y.(1)点E在边BC上运动的过程中,图中是否有相似三角形,请证明;
(2)求y关于x的函数解析式,并写出定义域;
(3)连接AF,点E在移动过程中,△AEF能否成为直角三角形?若能,请求出x的值;若不能,请说明理由.
分析 (1)根据题意证明∠BAE=∠CEF,根据相似三角形的判定定理证明即可;
(2)根据相似三角形的对应边成比例得到比例式,代入x、y计算即可;
(3)分∠EAF=90°和∠EFA=90°根据相似三角形的性质解答.
解答 解:(1)△ABE∽△ECF,
∵∠BAE+∠BEA=150°,∠CEF+∠BEA=150°,
∴∠BAE=∠CEF,又∠B=∠C,
∴△ABE∽△ECF;
(2)作AH⊥BC于H,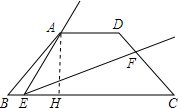
∵BC=4$\sqrt{3}$,AD=$\sqrt{3}$,
∴BH=$\frac{3\sqrt{3}}{2}$,又∠B=30°,
∴AB=3,
∵△ABE∽△ECF,
∴$\frac{AB}{EC}$=$\frac{BE}{CF}$,即$\frac{3}{4\sqrt{3}-x}$=$\frac{x}{y}$,
整理得,y=-$\frac{1}{3}$x2+$\frac{4\sqrt{3}}{3}$x(0≤x<4$\sqrt{3}$);
(3)当∠EAF=90°时,
∵∠AEF=30°,
∴$\frac{AE}{EF}$=cos30°=$\frac{\sqrt{3}}{2}$,
∴$\frac{AB}{EC}$=$\frac{\sqrt{3}}{2}$,即$\frac{3}{4\sqrt{3}-x}$=$\frac{\sqrt{3}}{2}$,
解得,x=2$\sqrt{3}$;
当∠EFA=90°时,
∵∠AEF=30°,
∴$\frac{EF}{AE}$=cos30°=$\frac{\sqrt{3}}{2}$,
∴$\frac{EC}{AB}$=$\frac{\sqrt{3}}{2}$,即$\frac{4\sqrt{3}-x}{3}$=$\frac{\sqrt{3}}{2}$,
解得x=$\frac{5}{2}$$\sqrt{3}$.
点评 本题考查的是相似三角形的知识的综合运用,掌握相似三角形的判定定理和性质定理是解题的关键,注意分情况讨论思想的运用.

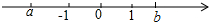
| A. | a<-a<b<-b<1 | B. | a<-b<b<1<-a | C. | a<b<-a<-b<1 | D. | a<-b<1<b<-a |
 如图,点O在线段AB上,AO=1,OB=2,OC为射线,且∠BOC=120°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC作匀速直线运动.设运动时间为t秒,当△ABP为直角三角形时,t的值为( )
如图,点O在线段AB上,AO=1,OB=2,OC为射线,且∠BOC=120°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC作匀速直线运动.设运动时间为t秒,当△ABP为直角三角形时,t的值为( )| A. | t=1 | B. | t=1或$\frac{-1+\sqrt{33}}{8}$ | C. | t=$\frac{1+\sqrt{33}}{8}$ | D. | t=1或$\frac{1+\sqrt{33}}{8}$ |
| A. | 3,3 | B. | 2,2 | C. | 2,3 | D. | 2,2.5 |
 如图,在正方形ABCD中AB=AD,∠B=∠D=90°.
如图,在正方形ABCD中AB=AD,∠B=∠D=90°.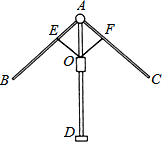 雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{2}$AB,AF=$\frac{1}{2}$AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=$\frac{1}{2}$AB,AF=$\frac{1}{2}$AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.