题目内容
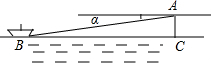如图所示，在某海岛上的观察所A发现海上某船只B并测得其俯角α=8°14′，已知观察所A的标高（当水位为0m时的高度）为43.74m，当时水位为+2.63m，求观察所A到船只B的水平距离BC．（精确到1m）分析：由题意可求得AC的长与∠BAC的度数，然后在Rt△ABC中，由tan81°46′=
，即可求得BC的长．
| BC |
| AC |
解答：解：当水位为+2.63m时，AC=43.74-2.63=41.11（m），
由题意得：α=8°14′，
∴∠BAC=90°-α=81°46′，
在Rt△ABC中，∵tan81°46′=
，
∴BC=AC•tan81°46′=41.11×6.911≈284（m）．
答：观察所A到船只B的水平距离BC为：284m．
由题意得：α=8°14′，
∴∠BAC=90°-α=81°46′，
在Rt△ABC中，∵tan81°46′=
| BC |
| AC |
∴BC=AC•tan81°46′=41.11×6.911≈284（m）．
答：观察所A到船只B的水平距离BC为：284m．
点评：此题考查了俯角的定义．注意能借助俯角构造直角三角形并解直角三角形是解此题的关键．
练习册系列答案
相关题目
于点A，连接OA．
于点B，连接BO交AP于C，设△AOP的面积为
，梯形BCPD的面积为
，则
