题目内容
9.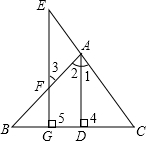 已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.
已知:如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3,试问:AD是∠BAC的平分线吗?若是,请说明理由.解:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直的定义)
∴AD∥EG(同位角相等,两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
∵∠E=∠3(已知)
∴∠1=∠2
∴AD是∠BAC的平分线(角平分线的定义)
分析 证明AD∥EG,得出∠1=∠E,∠2=∠3,再由已知得出∠1=∠2即可.
解答 解:是,理由如下:
∵AD⊥BC,EG⊥BC(已知)
∴∠4=∠5=90°(垂直的定义)
∴AD∥EG(同位角相等,两直线平行)
∴∠1=∠E(两直线平行,同位角相等)
∠2=∠3(两直线平行,内错角相等)
∵∠E=∠3(已知)
∴∠1=∠2,
∴AD是∠BAC的平分线(角平分线的定义);
故答案为:同位角相等,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;∠1,∠2.
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质,注意两者的区别.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17.如果方程组$\left\{\begin{array}{l}{x=2}\\{ax+by=7}\end{array}\right.$的解与方程组$\left\{\begin{array}{l}{y=3}\\{bx+ay=8}\end{array}\right.$的解相同,则a、b的值是( )
| A. | $\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=-2}\\{b=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=-2}\\{b=-1}\end{array}\right.$ |
14.今年3月12日,某学校开展植树活动,某植树小组20名同学的年龄情况如下表:
则这20名同学年龄的众数和中位数分别是( )
| 年龄(岁) | 12 | 13 | 14 | 15 | 16 |
| 人数 | 1 | 4 | 3 | 5 | 7 |
| A. | 15,14 | B. | 15,15 | C. | 16,14 | D. | 16,15 |
1.在实数-1,0,3,$\frac{1}{2}$中,最大的数是( )
| A. | -1 | B. | 0 | C. | 3 | D. | $\frac{1}{2}$ |
18.下列运算正确的是( )
| A. | (x-y)2=x2-y2 | B. | |$\sqrt{3}$-2|=2-$\sqrt{3}$ | C. | $\sqrt{8}$-$\sqrt{3}$=$\sqrt{5}$ | D. | -(-a+1)=a+1 |
 如图,四边形ABCD是矩形,C在x轴上,A(-1,0),B(0,2),双曲线y=$\frac{k}{x}$经过点D,则k的值为-6.
如图,四边形ABCD是矩形,C在x轴上,A(-1,0),B(0,2),双曲线y=$\frac{k}{x}$经过点D,则k的值为-6.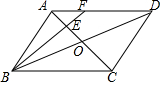 如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
如图,在?ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①$\frac{AF}{FD}$=$\frac{1}{2}$;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )