题目内容
如图，在等边△ABC中，M、N分别是边AB，AC的中点，D为MN上任意一点，BD，CD的延长线分别交于AB，AC于点E，F．若
=6，则△ABC的边长为
- A.
- B.
- C.
- D.1
C
分析：过点A作直线PQ∥BC，延长BE交PQ于点P；延长CF，交PQ于点Q．证明△BCE∽△PAE，△CBF∽△QAF，
构造
+
与BC的关系求解．
解答：
解：过点A作直线PQ∥BC，延长BD交PQ于点P；延长CD，交PQ于点Q．
∵D在MN上，PQ=BC，AE=AC-CE，AF=AB-BF，
在△BCE与△PAE中，∠PAE=∠ACB，∠APE=∠CBE，
∴△BCE∽△PAE，
=
…①
同理：△CBF∽△QAF，
=
…②
①+②，得：
+
=
．
∴
+
=3，
又∵=6，AC=AB，
∴△ABC的边长=．
故选C．
点评：本题综合考查了三角形中位线定理及三角形的相似的知识，解题的关键是作平行线构造相似，从而得到已知与所求线段的关系．
分析：过点A作直线PQ∥BC，延长BE交PQ于点P；延长CF，交PQ于点Q．证明△BCE∽△PAE，△CBF∽△QAF，
构造
+与BC的关系求解．解答：
解：过点A作直线PQ∥BC，延长BD交PQ于点P；延长CD，交PQ于点Q．∵D在MN上，PQ=BC，AE=AC-CE，AF=AB-BF，
在△BCE与△PAE中，∠PAE=∠ACB，∠APE=∠CBE，
∴△BCE∽△PAE，
=…①同理：△CBF∽△QAF，
=…②①+②，得：
+=．∴
+=3，又∵
=6，AC=AB，∴△ABC的边长=
．故选C．
点评：本题综合考查了三角形中位线定理及三角形的相似的知识，解题的关键是作平行线构造相似，从而得到已知与所求线段的关系．
练习册系列答案
相关题目
16、如图，在等边△ABC的边BC上任取一点D，作∠ADE=60°，DE交∠C的外角平分线于E，则△ADE是
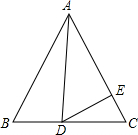如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
21、如图，在等边△ABC中，AD是∠BAC的平分线，点E在AC边上，且∠EDC=15°．
如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE=CD，AB=10cm．
如图，在等边△ABC中，BF是高，D是BF上一点，且OF=AF，作OE⊥BF，垂足为D，且OE=OB，连AE、AO、BE，求证：