Question

【题目】如图，抛物线y＝﹣x2+6x﹣5与x轴交于A，B两点（点A在点B左边），与y轴交于点C．点P是抛物线上一个动点，过点P作x轴的垂线，垂足为点H，交直线BC于点E．

（1）求点A，B，C的坐标；

（2）连接CP，当CP平分∠OCB时，求点P的坐标；

（3）平面直角坐标系内是否存在点Q，使得以点P，E，B，Q为顶点的四边形为菱形？若存在，直接写出点Q的坐标；若不存在，说明理由．

Answer 1

【答案】（1）点C的坐标为（0，﹣5）；（2）当CP平分∠OCB时，点P的坐标为（5，42）；（3）存在点Q，使以点P，E，B，Q为顶点的四边形为菱形．此时点Q的坐标为（﹣1，0），（5，52），（5，﹣4）或（5，﹣2﹣5）．

【解析】

（1）令y=0，求出x的值，即可得A、B两点坐标，令x=0，求出y的值，即可得C得坐标；（2）由PE⊥x轴可得PE//OC，即可证明∠OCP＝∠CPE，由CP平分∠OCB即可证明∠PCE＝∠CPE，可得PE=CE，根据B、C坐标可得OB=OC、直线BC的解析式，设P（x，﹣x2+6x﹣5），可得点E的坐标为（x，x﹣5），根据OB=OC可得CE=x，根据PE=CE列方程求出x的值即可得答案；（3）设P（x，﹣x2+6x﹣5），则E（x，x﹣5），当BQ为对角线时，根据菱形的性质可得BQ⊥PE，由PE⊥x轴可得点Q在x轴上，可得PH=EH，可求出H点坐标，根据BH=QH即可得Q点坐标；当点P在x轴上方时，PE＝EB＝BQ＝QP，分别用x表示出PE、BE的长，列方程求出x的值即可；当点P与点A重合时，根据PE=AB，可得E点坐标，由PB＝PE＝EQ＝QB，∠EAB=90°，即可得Q点坐标；当点P在x轴下方时，PE＝EB＝BQ＝QP，分别用x表示出PE、BE的长，列方程求出x的值即可；综上即可得答案.

（1）抛物线y＝﹣x2+6x﹣5与x轴交于A，B两点（点A在点B左边），与y轴交于点C

令y＝0时，得﹣x2+6x﹣5＝0，解得x1＝1，x2＝5，

∴点A的坐标为（1，0），点B的坐标为（5，0）

令x＝0时，y＝﹣5，

∴点C的坐标为（0，﹣5）

（2）当CP平分∠OCB时，∠OCP＝∠ECP，

∵PE⊥x轴，

∴PE//OC，

∴∠OCP＝∠CPE，

∴∠PCE＝∠CPE，

∴PE＝EC．

由题意可得直线BC的解析式为y＝x﹣5

设点P的坐标为（x，﹣x2+6x﹣5），则点E的坐标为（x，x﹣5），

∴PE＝﹣x2+6x﹣5﹣（x﹣5）＝﹣x2+5x．

∵B（5，0），C（0，-5），

∴OB＝OC=5，

∴CE=OH，

∴CE=x，

∴﹣x2+5x=x，

解得x1＝0（不合题意），x2＝5，

当x＝5时，﹣x2+6x﹣5＝42．

∴当CP平分∠OCB时，点P的坐标为（5，42）；

（3）存在点Q，使以点P，E，B，Q为顶点的四边形为菱形．此时点Q的坐标为（﹣1，0），（5，52），（5，﹣4）或（5，﹣2﹣5）

理由如下：

设点P的坐标为（x，﹣x2+6x﹣5），则点E的坐标为（x，x﹣5），

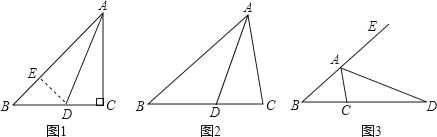
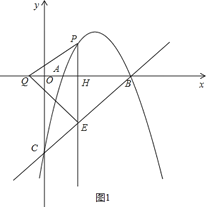
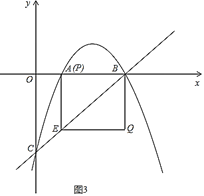
如图1，当BQ为对角线时：

∵PQEB是菱形，

∴PE⊥QB，PH＝HE，QH＝HB，

∴点Q在x轴上，

此时yP＝﹣yE，即﹣x2+6x﹣5＝﹣（x﹣5），

解得x1＝2，x2＝5（不合题意，舍去），

∴H（2，0），

∴QH＝HB＝3，

∴点Q的坐标为（﹣1，0）．

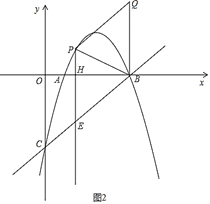
如图2，当点P在x轴上方，且PE＝EB＝BQ＝QP时，四边形PEBQ为菱形．

∵PE＝﹣x2+6x﹣5﹣（x﹣5）＝﹣x2+5x，BE=BH（5﹣x），

∴﹣x2+5x（5﹣x），

解得x1＝5（不合题意，舍去），x2．

当x时，BQ＝PE＝52，

∴点Q的坐标为（5，52）．

如图3，当点P与点A重合时，PB＝PE．

∴E点坐标为（1，-4），

∵PB＝PE＝EQ＝QB，∠EAB=90°，

∴Q的坐标为（5，﹣4）．

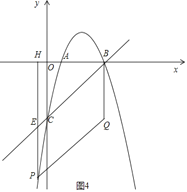
如图4，当点P在x轴下方，且PE＝EB＝BQ＝QP时，四边形PEBQ为菱形．

∵PE＝x﹣5﹣（﹣x2+6x﹣5）＝x2﹣5x，

BEBH（5﹣x），

∴x2﹣5x（5﹣x），

解得x1＝5（不合题意，舍去），x2．

当x时，QB＝PE＝2+5，

∴点Q的坐标为（5，﹣2﹣5）．

综上所述，存在点Q，使以点P，E，B，Q为顶点的四边形为菱形．此时点Q的坐标为（﹣1，0），（5，52），（5，﹣4）或（5，﹣2﹣5）．