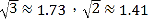Question

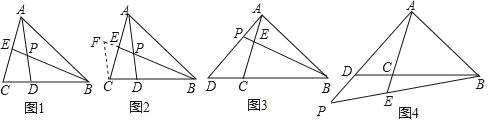
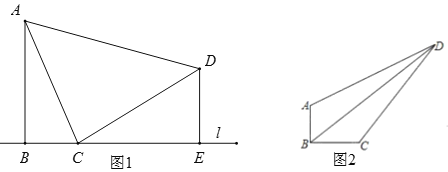
【题目】（1）如图1，已知AB⊥l，DE⊥l，垂足分别为B、E，且C是l上一点，∠ACD=90°．求证：△ABC∽△CED；

（2）如图2，在四边形ABCD中，∠ABC=90°，AB=6，BC=8，CD=20，DA=．求BD的长为_______．

Answer 1

【答案】(1)证明见解析；(2)4.

【解析】

（1）先证明∠BAC＝∠DCE，根据相似三角形的判定△ABC∽△CED即可；

（2）利用勾股定理和相似三角形的判定和性质解答即可．

（1）∵AB⊥l，DE⊥l，∴∠ABC＝∠CED＝90°，∠ACB+∠BAC＝90°．

∵∠ACD＝90°，∴∠ACB+∠DCE＝90°，∴∠BAC＝∠DCE，∴△ABC∽△CED；

（2）如图，连接AC．过点D作DE⊥BC延长线于点E．

∵∠ABC＝90°，∴AC．

∵AD＝10，CD＝20，∴△ACD满足AC2+CD2＝AD2，∴∠ACD＝90°．

由（1）得：△ABC∽△CED，∴，∴CE＝12，DE＝16．

在Rt△BDE中，BD．

故答案为：．